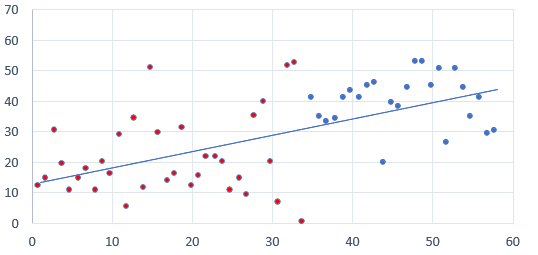
Linear regression is a fundamental statistical and machine learning technique used to model the relationship between a dependent variable (or target) and one or more independent variables (or predictors). The goal of linear regression is to predict the value of the target variable by fitting a linear equation to observed data points. This technique is one of the simplest yet most powerful methods in predictive analytics, widely used in various fields such as economics, finance, biology, and engineering.
The core idea behind linear regression is based on the concept of a linear relationship, where a change in the predictor variables results in a proportional change in the target variable. This assumption allows us to use a straight line to model the relationship between the variables. For instance, in a simple scenario where we want to predict house prices based on square footage, linear regression can help by establishing a line that best fits the data points, capturing the trend of how house prices vary with size.
In this article, we’ll cover the key concepts of linear regression, including the types of linear regression, the mathematical foundation behind it, and the assumptions that underpin the model. We’ll also explore its advantages, limitations, and some practical applications.
Key Concepts in Linear Regression
To understand linear regression, it’s essential to explore several foundational concepts, including dependent and independent variables, the linear model equation, and the loss function.
1. Dependent and Independent Variables
In linear regression, we focus on two types of variables:
- Dependent Variable: Also known as the target variable, this is the outcome we aim to predict. In a house pricing model, for instance, the dependent variable would be the price of the house.
- Independent Variable(s): Also called predictor(s) or feature(s), these are the input variables used to predict the dependent variable. In the housing price model, square footage, number of bedrooms, and location might serve as independent variables.
When there is a single independent variable, we refer to the model as simple linear regression. When there are multiple independent variables, it becomes a multiple linear regression model.
2. The Linear Model Equation
The linear regression model is represented by a linear equation that describes how the dependent variable changes with the independent variables. For simple linear regression with one predictor, the equation is:

where:
- y is the predicted value of the dependent variable.
- b0 is the intercept (the point where the line crosses the y-axis).
- b1 is the slope of the line, representing the change in y for a one-unit change in x.
- x is the independent variable.
- ε is the error term, accounting for the difference between the observed and predicted values.
For multiple linear regression with several predictors (x1,x2,……,xn), the equation expands to:
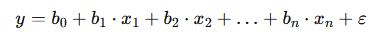
This model equation represents a hyperplane in a multidimensional space, where each predictor contributes to the prediction of y based on its coefficient (b1,b2,……,bn).
3. The Loss Function
In linear regression, the goal is to find the values of the coefficients (b0,b1,……,bn) that best fit the observed data. To measure the fit, we use a loss function—typically the mean squared error (MSE)—which calculates the average squared difference between the observed and predicted values.
The mean squared error is given by:

where:
- N is the number of observations.
- yi is the actual value of the dependent variable.
- yi^ is the predicted value from the model.
Minimizing the MSE allows us to find the optimal values for the coefficients that result in the best fit line or hyperplane. This process is typically done using an optimization algorithm such as gradient descent, which iteratively adjusts the coefficients to minimize the error.
Types of Linear Regression
There are several variations of linear regression, each suited to different types of data and scenarios. Here are the primary types:
1. Simple Linear Regression
Simple linear regression involves a single independent variable and models the relationship between this predictor and the target variable using a straight line. It is commonly used for straightforward predictive tasks where the goal is to understand the impact of one predictor.
- Example: Predicting a person’s height based on age. Here, height is the dependent variable, and age is the independent variable.
2. Multiple Linear Regression
In multiple linear regression, we use more than one independent variable to predict the target variable. This type of regression is suitable when multiple factors influence the outcome.
- Example: Predicting house prices based on square footage, number of rooms, and location. Here, house price is the dependent variable, and square footage, rooms, and location are independent variables.
3. Polynomial Regression
While linear regression assumes a straight-line relationship, polynomial regression allows for a curved relationship by incorporating polynomial terms. This type of regression is useful when the data exhibits a non-linear trend that a straight line cannot capture.
- Example: Modeling the growth of bacteria in a culture over time, where growth initially accelerates but then decelerates as resources are depleted. A polynomial regression with squared or cubic terms can capture this curved pattern.
4. Ridge and Lasso Regression
When dealing with multiple linear regression, adding too many predictors can lead to overfitting. Ridge regression and lasso regression are regularized versions of linear regression that help prevent overfitting by penalizing large coefficients.
- Ridge Regression: Adds a penalty term based on the sum of squared coefficients. This encourages smaller coefficients but does not eliminate them entirely.
- Lasso Regression: Adds a penalty term based on the sum of the absolute values of the coefficients, which can shrink some coefficients to zero, effectively selecting a subset of predictors.
Regularization techniques like ridge and lasso regression are especially useful in high-dimensional datasets, where there may be many predictors with varying degrees of relevance.
Assumptions of Linear Regression
Linear regression operates under several assumptions, which must be met for the model to produce reliable and accurate predictions:
- Linearity: The relationship between the predictors and the target variable should be linear. If the relationship is non-linear, the model may fail to capture the trend accurately.
- Independence: Observations in the dataset should be independent of each other. Dependencies between observations can bias the results, particularly in time series data.
- Homoscedasticity: The variance of errors should be constant across all levels of the independent variable(s). In other words, the spread of residuals (differences between observed and predicted values) should be similar across all predictions. If the error variance changes, this is called heteroscedasticity.
- Normality of Errors: The residuals should be normally distributed. This assumption is particularly important for inference (e.g., constructing confidence intervals) but less critical for prediction.
- No Multicollinearity (for multiple regression): Independent variables should not be highly correlated with each other. High correlations between predictors (multicollinearity) can make it difficult to estimate the relationship between each predictor and the target accurately.
Violations of these assumptions can reduce the effectiveness of the linear regression model. For instance, if the relationship between the variables is non-linear, polynomial regression or other non-linear models may be more appropriate.
Advantages of Linear Regression
Linear regression remains popular due to its simplicity, interpretability, and computational efficiency. Here are some of its primary advantages:
- Simplicity: Linear regression is straightforward to implement and easy to interpret. The relationship between the target and predictor variables can often be represented by a single equation, making it understandable for non-experts.
- Interpretability: The coefficients in linear regression provide insights into the relationship between each predictor and the target variable, allowing us to understand the magnitude and direction of each predictor’s influence.
- Efficiency: Linear regression models are computationally efficient, which makes them suitable for large datasets. The training process is often faster than for more complex models, especially with simple and multiple linear regression.
- Foundational: Linear regression serves as a foundation for more advanced techniques, such as logistic regression, polynomial regression, and support vector machines. Mastery of linear regression concepts provides a solid basis for understanding other machine learning methods.
Despite its simplicity, linear regression can be surprisingly powerful and is widely used for a variety of predictive tasks, from estimating sales trends to analyzing customer behavior.
Step-by-Step Guide to Implementing a Linear Regression Model
Building a linear regression model involves several steps, from preparing the data to training the model and evaluating its performance. Here’s a guide to help you implement a basic linear regression model:
Step 1: Prepare and Explore the Data
Before building the model, start by collecting, cleaning, and exploring the dataset. Ensuring data quality is crucial, as outliers, missing values, and inconsistencies can impact the accuracy of the linear regression model.
- Data Cleaning: Handle missing values, correct any data entry errors, and remove outliers that may skew the results.
- Exploratory Data Analysis (EDA): Visualize the relationships between the dependent and independent variables. Scatter plots, for example, can reveal whether a linear relationship exists, indicating whether linear regression is appropriate.
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# Load dataset
data = pd.read_csv("data.csv")
# Visualize relationship
sns.scatterplot(data=data, x="Independent_Variable", y="Dependent_Variable")
plt.show()Step 2: Split the Data into Training and Testing Sets
Splitting the data into training and testing sets allows us to evaluate the model’s performance on unseen data. A common split is 80% for training and 20% for testing.
from sklearn.model_selection import train_test_split
# Define predictors and target variable
X = data[["Independent_Variable1", "Independent_Variable2"]]
y = data["Dependent_Variable"]
# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)Step 3: Train the Model
Using a machine learning library like scikit-learn, training a linear regression model is straightforward. The model will calculate the optimal coefficients (b0,b1,……,bn) that minimize the error between the observed and predicted values.
from sklearn.linear_model import LinearRegression
# Initialize the linear regression model
model = LinearRegression()
# Fit the model to the training data
model.fit(X_train, y_train)Step 4: Make Predictions
Once the model is trained, we can use it to make predictions on the testing set. These predictions allow us to assess how well the model generalizes to new data.
# Make predictions on the test set
y_pred = model.predict(X_test)Step 5: Evaluate Model Performance
Evaluating the model’s performance involves measuring how accurately it predicts the target variable. Common evaluation metrics for linear regression include Mean Absolute Error (MAE), Mean Squared Error (MSE), and R-squared.
- Mean Absolute Error (MAE): The average absolute difference between the observed and predicted values.
- Mean Squared Error (MSE): The average squared difference between the observed and predicted values.
- R-squared: Indicates the proportion of the variance in the dependent variable that is predictable from the independent variables.
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
# Calculate evaluation metrics
mae = mean_absolute_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f"Mean Absolute Error: {mae}")
print(f"Mean Squared Error: {mse}")
print(f"R-squared: {r2}")These metrics provide insights into how well the model fits the data and whether it generalizes well to new observations.
Evaluating the Performance of a Linear Regression Model
Evaluating a linear regression model requires interpreting the values of performance metrics and understanding how well the model aligns with its assumptions.
1. Mean Absolute Error (MAE) and Mean Squared Error (MSE)
Both MAE and MSE measure the average difference between predicted and observed values, but they differ in sensitivity to outliers. MSE gives more weight to larger errors due to squaring, making it useful when large errors are especially costly or need emphasis.
- Interpreting MAE and MSE: Smaller values indicate a closer fit between predictions and actual values. When choosing between MAE and MSE, consider the application’s tolerance for outliers and the need to penalize large deviations.
2. R-squared (Coefficient of Determination)
R-squared is a widely used metric that measures how much of the variability in the target variable is explained by the model. It ranges from 0 to 1, with higher values indicating better explanatory power.
- Interpreting R-squared: An R-squared value close to 1 suggests that the model captures much of the variance in the data, while a low R-squared may indicate a poor fit. However, a high R-squared alone doesn’t guarantee a good model; it’s also essential to evaluate the model’s assumptions and performance on new data.
3. Residual Analysis
To assess the validity of the linear regression assumptions, examine the residuals (differences between observed and predicted values). Plotting residuals can reveal patterns, heteroscedasticity, or other issues that violate the assumptions of linearity and homoscedasticity.
- Normality of Residuals: For reliable confidence intervals and significance tests, residuals should be normally distributed. This can be checked using a histogram or Q-Q plot.
- Homoscedasticity: Residuals should have constant variance across the predicted values. A residuals vs. fitted values plot can help detect any patterns indicating heteroscedasticity.
import matplotlib.pyplot as plt
import numpy as np
# Plot residuals
residuals = y_test - y_pred
plt.scatter(y_pred, residuals)
plt.xlabel("Predicted Values")
plt.ylabel("Residuals")
plt.title("Residual Plot")
plt.axhline(0, color="red", linestyle="--")
plt.show()Practical Applications of Linear Regression
Linear regression is widely used across various industries due to its simplicity, interpretability, and effectiveness in predicting continuous outcomes. Here are some practical applications:
1. Predicting Sales and Revenue
Businesses frequently use linear regression to forecast sales, revenue, and other financial metrics based on historical data. By analyzing factors like advertising spend, seasonal trends, and product prices, companies can make informed decisions about future strategies.
- Example: A retail company might use linear regression to predict monthly sales based on advertising budgets, holiday seasons, and market trends. This helps allocate marketing resources effectively to maximize revenue.
2. Real Estate Valuation
In real estate, linear regression is used to predict property values based on factors such as location, square footage, number of bedrooms, and neighborhood amenities. This approach is especially useful for appraisers, investors, and real estate professionals.
- Example: A real estate agency might use multiple linear regression to estimate the value of homes in a specific area. By factoring in size, location, and nearby schools, the agency can provide accurate property valuations for clients.
3. Risk Assessment and Credit Scoring
Banks and financial institutions use linear regression to assess credit risk and determine credit scores for loan applicants. By analyzing factors like income, employment history, and credit history, they can estimate the likelihood of default.
- Example: A bank could use linear regression to determine a credit score based on a borrower’s income, debt-to-income ratio, and payment history. This score helps the bank decide whether to approve a loan and what interest rate to offer.
4. Demand Forecasting in Supply Chain
Manufacturers and suppliers use linear regression to forecast product demand based on historical sales, seasonality, and other influencing factors. Accurate demand forecasting helps optimize inventory levels and reduce stockouts or overstock situations.
- Example: A manufacturer of consumer electronics may use linear regression to predict demand for products like smartphones and laptops. By understanding demand patterns, the company can manage production schedules and supply chain logistics more efficiently.
5. Analyzing Health and Medical Data
In healthcare, linear regression is used to predict health outcomes, identify risk factors, and analyze the impact of treatments. This technique helps clinicians make data-driven decisions and improves patient care.
- Example: Linear regression can be used to analyze the relationship between body mass index (BMI) and blood pressure. By quantifying the effect of BMI on blood pressure, doctors can better advise patients on lifestyle changes to manage hypertension.
These applications demonstrate the versatility of linear regression, which can provide valuable insights and predictive power across diverse domains. While linear regression is often effective in these contexts, it’s essential to validate that the assumptions hold for each application and to consider alternative models if the relationships are non-linear or complex.
Limitations of Linear Regression
While linear regression is a powerful and widely-used modeling tool, it has certain limitations. Understanding these limitations helps determine when it’s appropriate to use linear regression and when other models may be more suitable.
1. Assumption of Linearity
One of the main limitations of linear regression is its reliance on the assumption of a linear relationship between the dependent and independent variables. In many real-world scenarios, relationships between variables are non-linear. When the linearity assumption doesn’t hold, the model can produce biased or inaccurate predictions.
- Example: In predicting house prices, if there is a non-linear relationship (e.g., exponential increase in value due to location or market demand), linear regression may fail to capture this trend effectively, resulting in under- or over-predictions.
2. Sensitivity to Outliers
Linear regression is sensitive to outliers—data points that significantly deviate from the overall pattern. Outliers can distort the model’s slope, intercept, and overall fit, leading to inaccurate predictions.
- Example: In a dataset of employee salaries, an outlier with an exceptionally high salary (such as a CEO’s income) can skew the results, making the model less representative of general employee salaries.
3. Multicollinearity in Multiple Linear Regression
In multiple linear regression, multicollinearity occurs when independent variables are highly correlated with each other. This correlation can make it challenging to determine the individual effect of each predictor, as multicollinearity reduces the precision of coefficient estimates and can lead to unstable predictions.
- Example: In a health study, if both age and years of experience are used as predictors of income, these variables may be highly correlated. Multicollinearity can obscure their individual contributions, affecting the reliability of the model.
4. Limited Applicability to Categorical Variables
Linear regression is not well-suited for categorical target variables. If the dependent variable is categorical (e.g., a yes/no outcome), linear regression isn’t appropriate. Logistic regression or other classification models are better suited for these types of problems.
- Example: In predicting whether a loan will be approved or denied, the binary nature of the target variable (approve/deny) makes logistic regression more appropriate than linear regression.
5. Assumption of Homoscedasticity
Linear regression assumes homoscedasticity, or constant variance of residuals across all levels of the independent variables. In real-world data, however, heteroscedasticity (variable spread of residuals) is common, leading to inaccurate confidence intervals and test statistics in the model.
- Example: In economic data, as income increases, the variance in spending might also increase, leading to heteroscedasticity that violates the linear regression assumption.
These limitations suggest that while linear regression is effective in many cases, other models may be needed for scenarios involving non-linear relationships, categorical data, or high variance across different levels of predictors.
Alternative Models for Non-Linear Data
When linear regression does not capture the complexity of the data, alternative models can be considered. Here are some commonly used models for handling non-linear relationships and complex patterns:
1. Polynomial Regression
Polynomial regression is an extension of linear regression that allows for curved relationships by including polynomial terms. Instead of fitting a straight line, polynomial regression fits a curve, making it more flexible for non-linear data.
- Example: In growth modeling, where a variable grows quickly and then stabilizes, a polynomial regression (e.g., quadratic or cubic) can better capture this trend than a straight line.
2. Decision Trees and Random Forests
Decision trees are non-linear models that split data into subsets based on decision rules, creating branches and leaves that represent different outcomes. Random forests, an ensemble of decision trees, average the predictions of multiple trees, reducing overfitting and improving accuracy.
- Example: In predicting customer churn, a random forest model can capture complex interactions between factors like purchase frequency, customer support interactions, and subscription plans.
3. Support Vector Machines (SVM)
Support Vector Machines can handle non-linear relationships by mapping data to higher-dimensional spaces using a technique called the kernel trick. This approach allows SVMs to create non-linear decision boundaries for classification tasks.
- Example: In classifying different types of flowers based on petal length and width, an SVM with a radial basis function (RBF) kernel can create a non-linear boundary that better separates flower species.
4. Neural Networks
Neural networks are powerful models capable of capturing complex non-linear patterns in data. With multiple layers of neurons, neural networks can learn intricate relationships and generalize well to a variety of tasks, from image recognition to natural language processing.
- Example: In predicting stock prices based on a variety of market indicators, a neural network can learn complex interactions between variables, making it more effective than linear regression for financial forecasting.
5. Logistic Regression (for Categorical Targets)
For tasks with a binary or categorical target variable, logistic regression is an alternative to linear regression. Logistic regression models the probability of a binary outcome (such as yes/no or success/failure) using a logistic function.
- Example: In medical diagnosis, logistic regression is used to predict whether a patient has a particular disease based on indicators like blood pressure, age, and cholesterol levels.
These models offer flexibility beyond linear regression, making them useful for tasks where data complexity or structure demands more sophisticated approaches.
Best Practices for Using Linear Regression
To achieve accurate and reliable results with linear regression, it’s important to follow certain best practices. These guidelines help ensure that the model is well-suited to the data and performs effectively in real-world applications.
1. Perform Exploratory Data Analysis (EDA)
Conducting a thorough exploratory data analysis helps identify the relationships between variables and ensures that linear regression is appropriate. Visualizations such as scatter plots and correlation matrices reveal potential patterns and relationships in the data.
- Best Practice: Use scatter plots to examine the relationship between the dependent and independent variables. A linear trend in the plot indicates that linear regression may be suitable.
2. Check for Multicollinearity
In multiple linear regression, checking for multicollinearity among predictors ensures that each variable contributes independently to the target. High multicollinearity can be identified through correlation matrices or variance inflation factor (VIF) values.
- Best Practice: If multicollinearity is present, consider removing or combining highly correlated variables, or use regularization techniques like ridge or lasso regression to mitigate its effects.
3. Address Outliers and Anomalies
Outliers can skew linear regression models, leading to biased estimates. Use box plots and statistical tests to identify and address outliers before training the model.
- Best Practice: Remove or transform outliers based on domain knowledge. In some cases, robust regression techniques that minimize the influence of outliers can be more effective than standard linear regression.
4. Transform Non-Linear Relationships
If a non-linear relationship is observed between the predictors and target variable, applying transformations to the variables (e.g., log, square root) can sometimes linearize the relationship, making it suitable for linear regression.
- Best Practice: Use transformations like logarithmic scaling or polynomial features to improve model fit in cases where linear regression alone is insufficient.
5. Regularize When Necessary
In cases with a large number of predictors, regularization techniques like ridge and lasso regression help prevent overfitting by penalizing large coefficients, ensuring the model generalizes well to new data.
- Best Practice: Apply ridge regression for datasets with many predictors to control the impact of multicollinearity. Use lasso regression for feature selection, as it can shrink less important predictors to zero.
6. Validate Model Assumptions
Validate that the linear regression model assumptions hold to ensure accurate predictions and statistical validity. Use diagnostic plots to assess linearity, homoscedasticity, normality of residuals, and independence.
- Best Practice: Perform residual analysis to check the model’s assumptions. If assumptions are violated, consider alternative models or transformations to address the issues.
7. Regularly Update and Monitor the Model
In dynamic environments where data patterns change over time, updating the linear regression model regularly ensures that predictions remain accurate. Monitoring the model’s performance over time helps detect issues such as data drift.
- Best Practice: Set up a schedule for periodic model updates and retrain with new data when necessary, especially in applications like sales forecasting and risk assessment where data can shift over time.
By following these best practices, practitioners can maximize the effectiveness of linear regression, ensuring the model is robust, interpretable, and capable of making accurate predictions.
The Value of Linear Regression in Predictive Analytics
Linear regression remains a foundational tool in machine learning and statistics, valued for its simplicity, interpretability, and computational efficiency. As one of the most accessible modeling techniques, it provides insights into the relationships between variables and enables predictions in various fields, from finance and healthcare to real estate and retail.
While linear regression has limitations, including sensitivity to outliers, reliance on linear relationships, and challenges with multicollinearity, alternative models like polynomial regression, decision trees, and neural networks offer solutions for more complex scenarios. Knowing when and how to use linear regression, as well as when to consider alternative approaches, is key to effective data-driven decision-making.
With best practices—such as performing exploratory data analysis, addressing multicollinearity, and validating model assumptions—practitioners can use linear regression to deliver valuable, reliable insights. Whether forecasting demand, analyzing health outcomes, or assessing risk, linear regression continues to play an essential role in modern predictive analytics, offering a straightforward yet powerful approach to understanding and leveraging data.