The bias-variance tradeoff is the fundamental tension in machine learning between two sources of error: bias (error from overly simplistic assumptions causing underfitting) and variance (error from excessive sensitivity to training data causing overfitting). High bias models are too simple and miss patterns, while high variance models are too complex and memorize noise. The sweet spot minimizes total error by balancing both—models complex enough to capture patterns but simple enough to generalize to new data.
Introduction: The Fundamental Dilemma
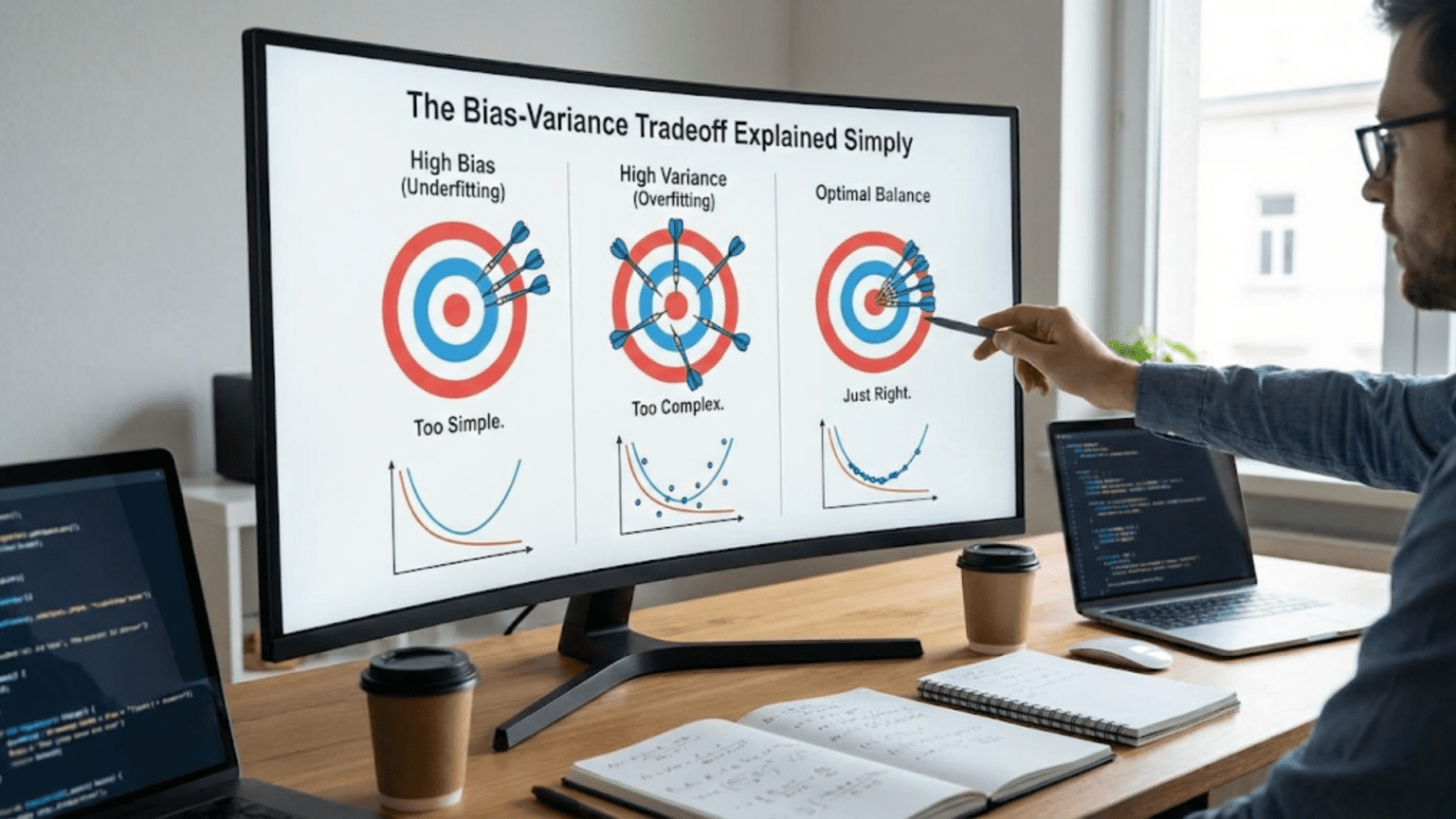
Imagine you’re trying to hit a target with darts. You throw many darts and observe two different patterns of misses. In the first pattern, all your darts cluster tightly together, but they’re consistently off-center—they’re precise but inaccurate. In the second pattern, your darts scatter widely around the target—sometimes close, sometimes far, but averaging near the center. Which is better? Neither is ideal. You want darts that cluster tightly AND center on the target.
Machine learning faces exactly this challenge. The bias-variance tradeoff is the formal description of why getting good predictions is so difficult. It explains why simple models often fail, why complex models also fail, and why finding the right balance is the core challenge of machine learning.
Bias and variance aren’t just abstract statistical concepts—they’re the two fundamental sources of prediction error that you’re constantly fighting when building models. Understanding this tradeoff transforms how you think about model selection, why certain approaches work, and how to diagnose and fix poor performance.
Every decision you make in machine learning—choosing algorithms, selecting features, tuning hyperparameters, regularizing models—is ultimately about navigating the bias-variance tradeoff. Too much bias and your model is too simple, missing important patterns in the data. Too much variance and your model is too complex, learning noise instead of signal.
This comprehensive guide explains the bias-variance tradeoff from the ground up. You’ll learn what bias and variance are, how they contribute to error, why they work against each other, how to diagnose which you’re suffering from, and practical strategies to find the optimal balance. With clear explanations, visual examples, and real-world applications, you’ll develop the intuition to navigate this fundamental machine learning challenge.
Understanding Error: The Components
Before understanding bias and variance, we need to understand prediction error.
Total Error Decomposition
Prediction Error on a new example has three components:
Total Error = Bias² + Variance + Irreducible ErrorIrreducible Error (also called noise):
- Inherent randomness in the problem
- Cannot be reduced no matter how good your model
- From measurement errors, unmeasured factors, true randomness
- Example: Predicting tomorrow’s weather—some uncertainty is fundamental
Reducible Error: Bias² + Variance
- Can be improved through better modeling
- This is what we focus on
The Tradeoff:
- Reducing bias often increases variance
- Reducing variance often increases bias
- Must balance both to minimize total error
What is Bias? The Underfitting Error
Bias is the error from overly simplistic assumptions in the learning algorithm. It represents how far off the model’s average predictions are from the true values.
Conceptual Understanding
High Bias Model:
- Makes strong assumptions about data
- Too simple to capture true patterns
- Systematically wrong in the same direction
- Underfits the data
Analogy: Using a ruler to trace a circle
- The ruler (linear model) is fundamentally too limited
- No matter how carefully you try, you can’t capture the curve
- You’ll consistently miss the true shape
Visual Example
True Relationship: Quadratic curve (y = x²)
High Bias Model: Straight line (y = mx + b)
True curve: /‾‾‾\
| |
/ \
Linear fit: /
/
/
Systematic error: Line can't capture curveEven with infinite training data, the line can’t fit the curve. This is bias.
Mathematical Understanding
Bias: Expected difference between model’s predictions and true values
Where:
- f̂(x) = model’s prediction
- f(x) = true value
- E[…] = expected value (average across many training sets)
High Bias: Model consistently predicts too high or too low
Example:
True value: 100
Model's predictions across different training sets:
Training set 1: 75
Training set 2: 73
Training set 3: 76
Training set 4: 74
Average: 74.5
Bias = 74.5 - 100 = -25.5 (consistently underestimates)Characteristics of High Bias
Performance Pattern:
- Poor training performance
- Poor test performance
- Similar errors on both training and test
- Underfitting
Model Characteristics:
- Too simple
- Too few parameters
- Strong assumptions
- High regularization
Examples:
- Linear regression for non-linear relationship
- Shallow decision tree for complex decision boundaries
- Naive Bayes assuming feature independence when features are highly correlated
- Small neural network for complex image recognition
Causes of High Bias
- Model too simple: Lacks capacity to represent true relationship
- Insufficient features: Missing important information
- Over-regularization: Penalty too strong, forcing model too simple
- Wrong assumptions: Model assumes patterns that don’t exist
Real-World Example: House Price Prediction
Scenario: Predicting house prices
High Bias Approach: Linear model with only one feature (square footage)
Price = 150 × sqft + 50,000Problem: Ignores location, condition, age, etc.
Result:
- Beach house: Predicts $500k, Actually $2M (underestimates)
- Rural house: Predicts $500k, Actually $200k (overestimates)
- Systematic errors because model too simple
What is Variance? The Overfitting Error
Variance is the error from sensitivity to small fluctuations in training data. It represents how much model predictions vary when trained on different datasets.
Conceptual Understanding
High Variance Model:
- Very flexible, few constraints
- Too complex, fits noise
- Changes dramatically with different training data
- Overfits the data
Analogy: Memorizing exam questions
- Student memorizes specific practice problems
- Changes completely with different practice set
- Doesn’t learn generalizable concepts
- Fails on actual exam with different questions
Visual Example
True Relationship: Smooth curve with noise
High Variance Model: Wiggly curve fitting every point
Training data: • • • • • • •
High variance: \_/\__/\/\_/\/
(fits every point, including noise)
New data: • • • • •
Same model: \_/\__/\/\_/\/
(terrible fit—learned noise not pattern)Mathematical Understanding
Variance: How much predictions vary across different training sets
Variance = E[(f̂(x) – E[f̂(x)])²]
High Variance: Predictions change dramatically with different training data
Example:
True value: 100
Model's predictions for same input across different training sets:
Training set 1: 120
Training set 2: 85
Training set 3: 135
Training set 4: 70
Average: 102.5 (close to true value)
But huge spread! Variance = E[(prediction - 102.5)²]
= (400 + 306.25 + 1056.25 + 1056.25) / 4 = 704.7
Model predictions are all over the placeCharacteristics of High Variance
Performance Pattern:
- Excellent training performance
- Poor test performance
- Large gap between training and test error
- Overfitting
Model Characteristics:
- Too complex
- Too many parameters
- Few assumptions
- Little/no regularization
Examples:
- High-degree polynomial regression
- Deep decision tree with no pruning
- Neural network with millions of parameters trained on thousands of examples
- k-NN with k=1 (nearest neighbor is always training point itself)
Causes of High Variance
- Model too complex: Too many parameters relative to data
- Insufficient training data: Can’t constrain complex model
- No regularization: Nothing prevents overfitting
- Training too long: Continues learning noise after patterns
Real-World Example: House Price Prediction
Scenario: Same house price prediction
High Variance Approach: 20th-degree polynomial with all possible feature interactions, tiny dataset (50 houses)
Problem: Model memorizes training houses exactly
Result:
- Training houses: Perfect predictions (zero error)
- New houses: Terrible predictions
- Small change in training data completely changes model
The Tradeoff: Why You Can’t Have Both Low
The fundamental challenge: reducing one increases the other.
The Seesaw Relationship
Complexity → Simple ..................... Complex
Bias → High ....................... Low
Variance → Low ........................ HighSimple Models:
- High bias (can’t capture patterns)
- Low variance (consistent predictions)
Complex Models:
- Low bias (can capture patterns)
- High variance (unstable predictions)
Why the Tradeoff Exists
Increasing Model Complexity:
Effect on Bias:
- More flexible model can fit true patterns better
- Fewer assumptions
- Bias decreases ↓
Effect on Variance:
- More parameters to tune from data
- More ways to fit noise
- More sensitive to training set specifics
- Variance increases ↑
Example:
Polynomial degree 1 (linear):
- Bias: High (can't fit curves)
- Variance: Low (stable line)
Polynomial degree 20:
- Bias: Low (can fit any curve)
- Variance: High (wiggly, unstable)The Sweet Spot
Optimal Complexity: Minimizes total error (bias² + variance)
Total Error
High │ \
│ \ /
│ \__________/
│ / \
Low │ / \
│____/________________\____
Simple Complex
↑
Sweet SpotLeft of Optimal: High bias dominates (underfitting) Right of Optimal: High variance dominates (overfitting) Optimal Point: Best balance, lowest total error
Practical Manifestation
Training Error:
Simple → Complex: High → Medium → Low → Very Low
(Decreases monotonically)Test Error:
Simple → Complex: High → Medium → Low → High again
(U-shaped curve)
↓
Sweet spotAt Sweet Spot:
- Training error: Moderate (not perfect)
- Test error: Minimized
- Small gap between training and test
- Best generalization
Diagnosing Bias vs. Variance Problems
How do you know which problem you have?
Diagnostic Framework
Check Training Performance:
Training Error High → High Bias Problem
Training Error Low → Potential Variance ProblemCheck Gap Between Training and Test:
Small Gap → Likely High Bias
Large Gap → Likely High VarianceFour Scenarios
Scenario 1: High Bias (Underfitting)
Symptoms:
Training Error: High (e.g., 30%)
Test Error: High (e.g., 32%)
Gap: Small (2%)Diagnosis: High bias, model too simple
Evidence: Can’t even fit training data well
Solution Direction: Increase complexity
Scenario 2: High Variance (Overfitting)
Symptoms:
Training Error: Very Low (e.g., 2%)
Test Error: High (e.g., 25%)
Gap: Large (23%)Diagnosis: High variance, model too complex
Evidence: Excellent on training, poor on test
Solution Direction: Reduce complexity or get more data
Scenario 3: High Bias AND High Variance
Symptoms:
Training Error: Moderate (e.g., 15%)
Test Error: High (e.g., 30%)
Gap: Large (15%)Diagnosis: Both problems
Evidence:
- Moderate training error (bias)
- Large gap (variance)
Solution: Tricky! Need to address both
Scenario 4: Good Balance (Sweet Spot)
Symptoms:
Training Error: Low-Moderate (e.g., 5%)
Test Error: Low-Moderate (e.g., 7%)
Gap: Small (2%)Diagnosis: Well-balanced model
Evidence: Good performance, small gap
Action: Deploy!
Diagnostic Table
| Training Error | Test Error | Gap | Diagnosis | Primary Issue |
|---|---|---|---|---|
| High | High | Small | Underfitting | High Bias |
| Low | Low | Small | Good Fit | Balanced |
| Very Low | High | Large | Overfitting | High Variance |
| Moderate | High | Large | Mixed | Both Bias & Variance |
Fixing High Bias: Reducing Underfitting
When diagnosis reveals high bias, increase model capacity.
Strategy 1: Increase Model Complexity
Actions:
For Neural Networks:
- Add more layers
- Add more neurons per layer
- Use more complex architectures
For Decision Trees:
- Allow deeper trees
- Reduce min_samples_split
- Reduce min_samples_leaf
For Polynomial Regression:
- Increase polynomial degree
Example:
# Before (high bias)
model = DecisionTreeClassifier(max_depth=3)
Training: 72%, Test: 70% (both poor)
# After (increase complexity)
model = DecisionTreeClassifier(max_depth=10)
Training: 85%, Test: 83% (both better)Strategy 2: Add More Features
Feature Engineering:
- Create interaction features
- Add polynomial features
- Engineer domain-specific features
- Include more raw features
Example:
# Before (3 features)
Features: [square_feet, bedrooms, bathrooms]
Accuracy: 70%
# After (10 features)
Features: [square_feet, bedrooms, bathrooms,
location, age, condition, garage,
square_feet × location,
age × condition]
Accuracy: 82%Strategy 3: Reduce Regularization
Decrease Regularization Strength:
# Before (strong regularization)
model = Ridge(alpha=100) # High penalty
# After (reduce penalty)
model = Ridge(alpha=0.1) # Lower penaltyReduce Dropout:
# Before (high dropout)
model.add(Dropout(0.8)) # Drops 80% of neurons
# After (reduce dropout)
model.add(Dropout(0.3)) # Drops only 30%Strategy 4: Train Longer
For iterative algorithms:
- Increase number of epochs
- Train until convergence
Example:
# Before (stopped too early)
model.fit(X, y, epochs=10)
# After (train longer)
model.fit(X, y, epochs=100)Strategy 5: Try Different Algorithm
Move to More Flexible Algorithm:
Linear Regression → Polynomial Regression
Logistic Regression → Random Forest
Shallow Neural Net → Deep Neural NetFixing High Variance: Reducing Overfitting
When diagnosis reveals high variance, reduce model sensitivity.
Strategy 1: Get More Training Data
Most Effective Solution:
- Collect more labeled examples
- Data augmentation (images, text)
- Synthetic data generation
Why It Works:
- More data harder to memorize
- Noise averages out
- True patterns become clearer
Example:
1,000 examples: Train=98%, Test=75% (overfit)
10,000 examples: Train=92%, Test=88% (better)
100,000 examples: Train=90%, Test=89% (excellent)Strategy 2: Reduce Model Complexity
Actions:
Neural Networks:
- Fewer layers
- Fewer neurons per layer
- Simpler architectures
Decision Trees:
- Limit max depth
- Increase min_samples_split
- Prune tree
Polynomial Regression:
- Reduce polynomial degree
Example:
# Before (too complex)
model = RandomForestClassifier(max_depth=None, min_samples_split=2)
Train: 98%, Test: 72%
# After (reduce complexity)
model = RandomForestClassifier(max_depth=10, min_samples_split=10)
Train: 88%, Test: 85%Strategy 3: Add Regularization
L1/L2 Regularization:
# Add regularization
model = Ridge(alpha=10) # L2
model = Lasso(alpha=0.1) # L1Dropout (Neural Networks):
model.add(Dense(128))
model.add(Dropout(0.5)) # RegularizationEarly Stopping:
early_stop = EarlyStopping(monitor='val_loss', patience=10)
model.fit(X, y, validation_data=(X_val, y_val), callbacks=[early_stop])Strategy 4: Feature Selection
Remove Irrelevant Features:
- Use feature importance
- Correlation analysis
- Recursive feature elimination
Example:
# Before (100 features, many irrelevant)
Train: 95%, Test: 70%
# After (20 most important features)
Train: 87%, Test: 84%Strategy 5: Ensemble Methods
Combine Multiple Models:
- Bagging (Random Forests) reduces variance
- Averaging predictions
- Each model overfits differently
Example:
# Single tree (high variance)
model = DecisionTreeClassifier()
Train: 100%, Test: 75%
# Random Forest (ensemble, lower variance)
model = RandomForestClassifier(n_estimators=100)
Train: 90%, Test: 86%Strategy 6: Cross-Validation
Use During Development:
- More robust performance estimates
- Less likely to overfit to validation set
Practical Example: Navigating the Tradeoff
Let’s walk through a complete example.
Problem Setup
Task: Predict customer churn Data: 5,000 customers, 30 features Baseline: Always predict “no churn” = 80% accuracy (naive)
Attempt 1: Logistic Regression (Too Simple)
Model: Simple logistic regression, 5 features
Results:
Training Accuracy: 81%
Test Accuracy: 80%
Gap: 1%Diagnosis:
- Both scores barely beat baseline
- Small gap
- High Bias: Model too simple
Evidence: Can’t even fit training data well
Attempt 2: Random Forest, No Limits (Too Complex)
Model: Random Forest with default settings (very deep trees)
Results:
Training Accuracy: 99%
Test Accuracy: 76%
Gap: 23%Diagnosis:
- Excellent training
- Poor test
- Large gap
- High Variance: Model overfitting
Evidence: Memorized training data
Attempt 3: Finding Balance
Systematic Approach: Try various complexities
Experiments:
max_depth=3: Train=82%, Test=81%, Gap=1% (still high bias)
max_depth=5: Train=85%, Test=84%, Gap=1% (better)
max_depth=7: Train=89%, Test=87%, Gap=2% (even better)
max_depth=10: Train=92%, Test=88%, Gap=4% (optimal!)
max_depth=15: Train=96%, Test=85%, Gap=11% (variance increasing)
max_depth=20: Train=98%, Test=82%, Gap=16% (high variance)
max_depth=None: Train=99%, Test=76%, Gap=23% (severe overfit)Optimal Choice: max_depth=10
- Training: 92% (good, not perfect)
- Test: 88% (best test performance)
- Gap: 4% (acceptable)
- Best bias-variance balance
Attempt 4: Further Optimization
Add Regularization to depth=10 model:
model = RandomForestClassifier(
max_depth=10,
min_samples_split=10, # Regularization
min_samples_leaf=5, # Regularization
n_estimators=100
)Results:
Training Accuracy: 90%
Test Accuracy: 89%
Gap: 1%
Analysis:
- Slightly lower training (90% vs 92%)
- Higher test (89% vs 88%)
- Smaller gap (1% vs 4%)
- Better generalization!
Learning Curves Analysis
Plot Training and Test Error vs. Model Complexity:
Error
High │ \ /
│ \ /
│ \____Test_______/
│ \ /
│ \____________/
Low │ \__Training_____
│__________________________
Simple Complex
↑
max_depth=10Observations:
- Left: High training AND test error (bias)
- Middle: Minimum test error (sweet spot)
- Right: Low training, high test error (variance)
Final Model
Configuration:
RandomForestClassifier(
max_depth=10,
min_samples_split=10,
min_samples_leaf=5,
n_estimators=100,
random_state=42
)Performance:
Training: 90%
Validation: 89%
Test: 88.5%Interpretation:
- Excellent test performance
- Small train-test gap
- Optimal bias-variance balance
- Ready for deployment
Advanced: Bias-Variance Decomposition
For regression, we can mathematically decompose error.
The Mathematics
For a point x with true value y:
Expected Error = Bias² + Variance + Noise
Where:
Bias² = (E[f̂(x)] - y)²
Variance = E[(f̂(x) - E[f̂(x)])²]
Noise = irreducible errorEmpirical Estimation
Process:
- Train many models on different training sets
- Make predictions on same test point
- Calculate bias and variance empirically
Example:
import numpy as np
from sklearn.tree import DecisionTreeRegressor
# True function: y = x²
def true_function(x):
return x**2
# Generate test point
x_test = 0.5
y_true = true_function(x_test)
# Train 100 models on different samples
predictions = []
for _ in range(100):
# Different random training set each time
X_train = np.random.uniform(-1, 1, 50).reshape(-1, 1)
y_train = true_function(X_train) + np.random.normal(0, 0.1, X_train.shape)
model = DecisionTreeRegressor(max_depth=5)
model.fit(X_train, y_train)
pred = model.predict([[x_test]])[0]
predictions.append(pred)
# Calculate components
mean_prediction = np.mean(predictions)
bias_squared = (mean_prediction - y_true)**2
variance = np.var(predictions)
mse = np.mean((predictions - y_true)**2)
print(f"Bias²: {bias_squared:.4f}")
print(f"Variance: {variance:.4f}")
print(f"MSE: {mse:.4f}")
print(f"Bias² + Variance: {bias_squared + variance:.4f}")Bias-Variance in Different Contexts
Classification
Bias: Systematic errors in class predictions
- High bias: Predicts wrong class consistently
- Example: Always predicts majority class
Variance: Prediction instability
- High variance: Class predictions change with training set
- Example: Decision boundary moves dramatically
Deep Learning
Bias:
- Network too small (few layers/neurons)
- Early stopping too aggressive
Variance:
- Network too large
- Training too long
- Insufficient data
Modern Trend: Deep networks with heavy regularization
- Large capacity (low bias potential)
- Regularization controls variance
- Best of both worlds
Ensemble Methods
Bagging (Random Forests): Reduces variance
- Train many high-variance models
- Average predictions
- Variance decreases, bias unchanged
Boosting: Reduces bias
- Sequentially train weak models
- Each corrects predecessor’s errors
- Bias decreases, some variance increase
Common Misconceptions
Misconception 1: “More Data Always Helps”
Truth: More data helps HIGH VARIANCE, not high bias
Example:
High bias (linear model for curved data):
1,000 examples: 70% accuracy
1,000,000 examples: 71% accuracy (minimal improvement)
Model is fundamentally too simple
High variance (complex model):
1,000 examples: 75% accuracy
1,000,000 examples: 92% accuracy (huge improvement)
More data constrains overfittingMisconception 2: “Complex Models Always Better”
Truth: Only if you have enough data
Example:
100 examples:
Simple model: 80% accuracy
Complex model: 70% accuracy (overfits)
100,000 examples:
Simple model: 81% accuracy (bias-limited)
Complex model: 92% accuracy (has data to learn)Misconception 3: “Zero Training Error is Good”
Truth: Zero training error usually means overfitting (high variance)
Healthy Model: Some training error acceptable
- Indicates model not memorizing
- Generalization capacity preserved
Misconception 4: “Regularization Always Helps”
Truth: Regularization helps high variance, hurts high bias
Too Much Regularization:
Causes: High bias (over-regularized)
Training error: High
Test error: High
Both are badBest Practices for Managing Bias-Variance Tradeoff
During Development
- Start Simple: Begin with simple model, increase complexity gradually
- Plot Learning Curves: Visualize train/test error vs. complexity
- Diagnose First: Identify whether bias or variance is the problem
- Apply Appropriate Fix: Don’t blindly add complexity or data
Model Selection
- Cross-Validation: Get robust estimates across multiple splits
- Multiple Metrics: Don’t rely on single number
- Validation Curve: Plot performance vs. hyperparameter values
- Learning Curve: Plot performance vs. training set size
Deployment
- Monitor Both Metrics: Track training and test/production performance
- Watch for Drift: Performance degradation signals changing patterns
- Retrain Periodically: Update with fresh data to maintain balance
Comparison: Strategies for Bias vs. Variance
| Problem | Symptoms | Solutions | What NOT to Do |
|---|---|---|---|
| High Bias | Training & test errors both high, small gap | Increase complexity, add features, reduce regularization, train longer | Add more data (won’t help much), increase regularization |
| High Variance | Training error low, test error high, large gap | Get more data, reduce complexity, add regularization, feature selection | Increase complexity, reduce regularization |
| Good Balance | Both errors acceptable, small gap | Maintain current approach, monitor | Over-optimize (risk breaking balance) |
| Both Issues | Moderate training error, high test error, large gap | Carefully add complexity AND data, neural nets with regularization | Simple solutions (need nuanced approach) |
Conclusion: The Central Challenge of Machine Learning
The bias-variance tradeoff isn’t just a theoretical concept—it’s the fundamental challenge underlying all of machine learning. Every time you adjust model complexity, select features, tune hyperparameters, or choose algorithms, you’re navigating this tradeoff.
Understanding bias and variance transforms how you approach machine learning:
Bias is error from oversimplification. High bias models make strong assumptions, miss patterns, and underfit. They’re consistently wrong, failing on both training and test data.
Variance is error from overcomplexity. High variance models are too sensitive to training data specifics, learn noise, and overfit. They excel on training data but fail to generalize.
The tradeoff exists because reducing one increases the other. Simple models have high bias but low variance. Complex models have low bias but high variance. The sweet spot balances both, minimizing total error.
Diagnosis is key. Look at training and test performance together:
- Both poor → high bias
- Training great, test poor → high variance
- Both good → optimal balance
Solutions differ by problem:
- High bias → increase complexity, add features, reduce regularization
- High variance → get more data, reduce complexity, add regularization
The goal isn’t eliminating bias and variance—it’s finding the right balance for your specific problem, data, and constraints. Sometimes you’ll accept higher bias for lower variance, or vice versa, depending on what matters for your application.
As you build machine learning systems, make bias-variance analysis a core part of your workflow. Plot learning curves. Diagnose which error dominates. Apply targeted solutions. Monitor the balance in production. This disciplined approach to managing the bias-variance tradeoff is what separates effective machine learning practitioners from those who struggle.
Master this fundamental tradeoff, and you’ve mastered the essence of machine learning—finding models that capture genuine patterns without memorizing noise, delivering robust performance on new data rather than just impressive numbers on training sets.