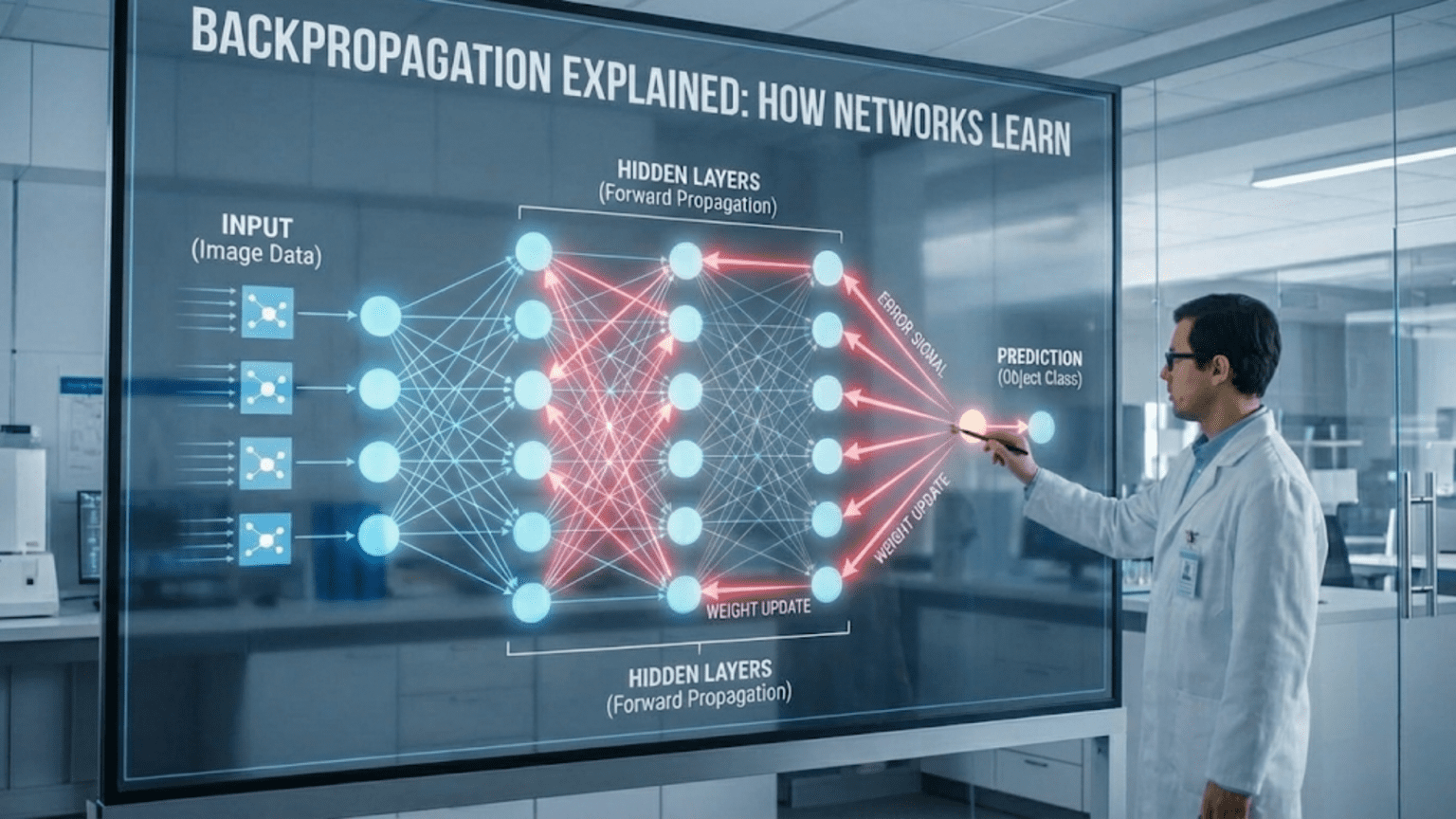
Backpropagation is the algorithm that enables neural networks to learn by computing how much each weight contributed to the prediction error and adjusting weights accordingly. It works by calculating the gradient of the loss function with respect to each weight through the chain rule, propagating error signals backward from output to input layer. Starting with the difference between prediction and actual value, backpropagation calculates how to adjust each weight to reduce error, enabling networks to iteratively improve through gradient descent.
Introduction: The Learning Algorithm That Changed AI
Imagine you’re trying to tune a complex machine with thousands of knobs. Each knob affects the output, but you don’t know which direction to turn each one to improve performance. Randomly adjusting knobs would take forever. What if you could somehow determine exactly which way to turn each knob and by how much? That’s what backpropagation does for neural networks.
Backpropagation (short for “backward propagation of errors”) is the algorithm that makes deep learning possible. Before its widespread adoption in the 1980s, training neural networks with multiple layers was impractical—no one knew how to efficiently adjust the millions of parameters these networks contain. Backpropagation solved this problem, providing an efficient way to calculate exactly how to adjust each weight to reduce error.
The algorithm is elegant in its simplicity: use calculus to determine how each weight affects the error, then adjust weights in the direction that reduces error. Yet this simple idea enables neural networks to learn incredibly complex patterns, from recognizing faces to understanding language to playing games at superhuman levels.
Understanding backpropagation is essential for anyone serious about deep learning. It’s not just theoretical—this is the actual mechanism by which networks improve. When you see a network’s accuracy improve during training, backpropagation is doing the work. When you adjust learning rates or try different optimizers, you’re modifying how backpropagation operates. When debugging why a network won’t train, understanding backpropagation helps diagnose the problem.
This comprehensive guide demystifies backpropagation. You’ll learn what it is, why it works, the mathematical foundations, step-by-step calculations through a complete example, implementation details, common problems and solutions, and intuitive understanding of this foundational algorithm.
The Problem: How to Adjust Millions of Weights
To appreciate backpropagation, we must first understand the challenge it solves.
The Learning Challenge
Given:
- Neural network with weights W and biases b
- Training data: inputs X and desired outputs Y
- Loss function measuring prediction error
Goal: Adjust W and b to minimize loss (error)
The Problem:
- Networks have thousands to billions of parameters
- How to know which direction to adjust each weight?
- How much to adjust each weight?
- Need efficient algorithm—can’t try random adjustments
The Naive Approach: Random Search
Method: Randomly adjust weights, keep changes that improve performance
Why It Fails:
Network with 1,000,000 weights
Each weight can increase or decrease
Search space: 2^1,000,000 possibilities
Even checking 1 billion combinations per second:
Would take longer than age of universe!Conclusion: Need smarter approach
The Key Insight: Gradients
Better Idea: Calculate gradient (derivative) of loss with respect to each weight
Gradient tells us:
- Which direction to adjust weight (increase or decrease)
- How much weight affects loss (sensitivity)
Mathematical Foundation:
∂Loss/∂w = how much loss changes when w changes
If ∂Loss/∂w > 0: Increasing w increases loss → decrease w
If ∂Loss/∂w < 0: Increasing w decreases loss → increase w
Update rule:
w_new = w_old - learning_rate × ∂Loss/∂wChallenge: How to efficiently calculate ∂Loss/∂w for every weight in deep networks?
Solution: Backpropagation!
What is Backpropagation?
Backpropagation is an efficient algorithm for computing gradients of the loss function with respect to all weights in a neural network.
The Core Idea
Forward Pass:
- Input → Hidden layers → Output → Prediction
- Calculate loss (error)
Backward Pass (Backpropagation):
- Start with loss
- Work backward through network
- Calculate how much each weight contributed to loss
- Compute gradient for every weight
The Name:
- “Backward” – goes from output to input (reverse of forward pass)
- “Propagation” – error signal propagates backward through network
How It Works: High-Level View
Step 1: Forward pass (make prediction)
Input → Layer 1 → Layer 2 → ... → Output → LossStep 2: Calculate output error
Error = Loss gradient = ∂Loss/∂outputStep 3: Backward pass (propagate error backward)
Output error → Layer N gradient → Layer N-1 gradient → ... → Layer 1 gradientStep 4: Update weights using gradients
For each layer:
W = W - learning_rate × ∂Loss/∂W
b = b - learning_rate × ∂Loss/∂bThe Mathematical Foundation: Chain Rule
Chain Rule of Calculus: Key to backpropagation
Simple Example:
If y = f(u) and u = g(x)
Then: dy/dx = (dy/du) × (du/dx)In Neural Networks:
Loss depends on output layer
Output layer depends on hidden layer
Hidden layer depends on input layer
Chain rule lets us decompose:
∂Loss/∂W₁ = (∂Loss/∂output) × (∂output/∂hidden) × (∂hidden/∂W₁)Why This Matters:
- Can compute gradients layer by layer
- Reuse intermediate calculations
- Efficient even for very deep networks
The Algorithm: Step-by-Step
Let’s walk through backpropagation in detail.
Notation
L = number of layers
l = layer index (1 to L)
W⁽ˡ⁾ = weight matrix for layer l
b⁽ˡ⁾ = bias vector for layer l
Z⁽ˡ⁾ = weighted sum at layer l (before activation)
A⁽ˡ⁾ = activation at layer l (after activation function)
f⁽ˡ⁾ = activation function for layer l
ℒ = loss functionForward Pass (Review)
For l = 1 to L:
Z⁽ˡ⁾ = W⁽ˡ⁾A⁽ˡ⁻¹⁾ + b⁽ˡ⁾
A⁽ˡ⁾ = f⁽ˡ⁾(Z⁽ˡ⁾)
A⁽⁰⁾ = X (input)
ŷ = A⁽ᴸ⁾ (prediction)
ℒ = Loss(ŷ, y) (loss)Backward Pass (Backpropagation)
Output Layer (Layer L):
Step 1: Compute derivative of loss with respect to output
dA⁽ᴸ⁾ = ∂ℒ/∂A⁽ᴸ⁾
Step 2: Compute derivative with respect to Z⁽ᴸ⁾
dZ⁽ᴸ⁾ = dA⁽ᴸ⁾ ⊙ f'⁽ᴸ⁾(Z⁽ᴸ⁾)
(⊙ = element-wise multiplication)
Step 3: Compute gradients for weights and biases
dW⁽ᴸ⁾ = dZ⁽ᴸ⁾ · (A⁽ᴸ⁻¹⁾)ᵀ / m
db⁽ᴸ⁾ = sum(dZ⁽ᴸ⁾) / m
(m = number of examples)
Step 4: Propagate error to previous layer
dA⁽ᴸ⁻¹⁾ = (W⁽ᴸ⁾)ᵀ · dZ⁽ᴸ⁾Hidden Layers (Layer l, for l = L-1 down to 1):
For each layer l (from L-1 down to 1):
Step 1: Compute dZ⁽ˡ⁾
dZ⁽ˡ⁾ = dA⁽ˡ⁾ ⊙ f'⁽ˡ⁾(Z⁽ˡ⁾)
Step 2: Compute gradients
dW⁽ˡ⁾ = dZ⁽ˡ⁾ · (A⁽ˡ⁻¹⁾)ᵀ / m
db⁽ˡ⁾ = sum(dZ⁽ˡ⁾) / m
Step 3: Propagate error backward
dA⁽ˡ⁻¹⁾ = (W⁽ˡ⁾)ᵀ · dZ⁽ˡ⁾Weight Update:
For each layer l:
W⁽ˡ⁾ = W⁽ˡ⁾ - α × dW⁽ˡ⁾
b⁽ˡ⁾ = b⁽ˡ⁾ - α × db⁽ˡ⁾
(α = learning rate)Complete Example: Backpropagation in Action
Let’s trace backpropagation through a simple network.
Network Setup
Architecture:
- Input: 2 features
- Hidden layer: 2 neurons (sigmoid activation)
- Output: 1 neuron (sigmoid activation)
- Loss: Mean Squared Error (MSE)
Training Example:
Input: X = [0.5, 0.8]
True output: y = 1Initial Weights (random):
W⁽¹⁾ = [[0.15, 0.25], b⁽¹⁾ = [0.35]
[0.20, 0.30]] [0.35]
W⁽²⁾ = [[0.40, 0.50]] b⁽²⁾ = [0.60]Learning rate: α = 0.5
Forward Pass
Layer 1:
Z⁽¹⁾ = W⁽¹⁾X + b⁽¹⁾
z₁⁽¹⁾ = (0.15×0.5) + (0.25×0.8) + 0.35 = 0.075 + 0.2 + 0.35 = 0.625
z₂⁽¹⁾ = (0.20×0.5) + (0.30×0.8) + 0.35 = 0.1 + 0.24 + 0.35 = 0.69
Z⁽¹⁾ = [0.625, 0.69]
A⁽¹⁾ = sigmoid(Z⁽¹⁾)
a₁⁽¹⁾ = σ(0.625) = 0.651
a₂⁽¹⁾ = σ(0.69) = 0.666
A⁽¹⁾ = [0.651, 0.666]Layer 2 (Output):
Z⁽²⁾ = W⁽²⁾A⁽¹⁾ + b⁽²⁾
z⁽²⁾ = (0.40×0.651) + (0.50×0.666) + 0.60
= 0.2604 + 0.333 + 0.60
= 1.1934
A⁽²⁾ = sigmoid(Z⁽²⁾)
a⁽²⁾ = σ(1.1934) = 0.767
ŷ = 0.767 (prediction)Loss:
ℒ = MSE = (y - ŷ)² / 2
= (1 - 0.767)² / 2
= (0.233)² / 2
= 0.0271Backward Pass
Output Layer:
Step 1: Loss gradient
∂ℒ/∂ŷ = -(y - ŷ) = -(1 - 0.767) = -0.233Step 2: Gradient with respect to Z⁽²⁾
Sigmoid derivative: σ'(z) = σ(z)(1 - σ(z))
dZ⁽²⁾ = ∂ℒ/∂ŷ × σ'(Z⁽²⁾)
= -0.233 × 0.767 × (1 - 0.767)
= -0.233 × 0.767 × 0.233
= -0.0416Step 3: Gradients for W⁽²⁾ and b⁽²⁾
dW⁽²⁾ = dZ⁽²⁾ × A⁽¹⁾ᵀ
= -0.0416 × [0.651, 0.666]
= [-0.0271, -0.0277]
db⁽²⁾ = dZ⁽²⁾
= -0.0416Step 4: Error to previous layer
dA⁽¹⁾ = W⁽²⁾ᵀ × dZ⁽²⁾
= [0.40, 0.50]ᵀ × -0.0416
= [0.40 × -0.0416] = [-0.0166]
[0.50 × -0.0416] [-0.0208]Hidden Layer:
Step 1: Gradient with respect to Z⁽¹⁾
dZ⁽¹⁾ = dA⁽¹⁾ ⊙ σ'(Z⁽¹⁾)
For neuron 1:
dz₁⁽¹⁾ = -0.0166 × 0.651 × (1 - 0.651)
= -0.0166 × 0.651 × 0.349
= -0.00377
For neuron 2:
dz₂⁽¹⁾ = -0.0208 × 0.666 × (1 - 0.666)
= -0.0208 × 0.666 × 0.334
= -0.00463
dZ⁽¹⁾ = [-0.00377, -0.00463]Step 2: Gradients for W⁽¹⁾ and b⁽¹⁾
dW⁽¹⁾ = dZ⁽¹⁾ × Xᵀ
Row 1: dw₁₁⁽¹⁾ = -0.00377 × 0.5 = -0.00189
dw₁₂⁽¹⁾ = -0.00377 × 0.8 = -0.00302
Row 2: dw₂₁⁽¹⁾ = -0.00463 × 0.5 = -0.00232
dw₂₂⁽¹⁾ = -0.00463 × 0.8 = -0.00370
dW⁽¹⁾ = [[-0.00189, -0.00302],
[-0.00232, -0.00370]]
db⁽¹⁾ = dZ⁽¹⁾ = [-0.00377, -0.00463]Weight Updates
Layer 2:
W⁽²⁾_new = W⁽²⁾ - α × dW⁽²⁾
= [0.40, 0.50] - 0.5 × [-0.0271, -0.0277]
= [0.40, 0.50] - [-0.0136, -0.0139]
= [0.4136, 0.5139]
b⁽²⁾_new = 0.60 - 0.5 × (-0.0416)
= 0.60 + 0.0208
= 0.6208Layer 1:
W⁽¹⁾_new = W⁽¹⁾ - α × dW⁽¹⁾
= [[0.15, 0.25], - 0.5 × [[-0.00189, -0.00302],
[0.20, 0.30]] [-0.00232, -0.00370]]
= [[0.15095, 0.25151],
[0.20116, 0.30185]]
b⁽¹⁾_new = [0.35, 0.35] - 0.5 × [-0.00377, -0.00463]
= [0.35189, 0.35232]Result After One Update
Before: Loss = 0.0271, Prediction = 0.767
After (with updated weights, re-run forward pass):
- Loss ≈ 0.0265 (reduced!)
- Prediction ≈ 0.772 (closer to true value of 1!)
Success: Weights moved in direction that reduces error!
Implementation: Python Code
NumPy Implementation
import numpy as np
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def sigmoid_derivative(z):
s = sigmoid(z)
return s * (1 - s)
def mse_loss(y_true, y_pred):
return np.mean((y_true - y_pred) ** 2)
def mse_loss_derivative(y_true, y_pred):
return -(y_true - y_pred)
class TwoLayerNetwork:
def __init__(self, input_size, hidden_size, output_size, learning_rate=0.5):
# Initialize weights randomly
self.W1 = np.random.randn(hidden_size, input_size) * 0.1
self.b1 = np.random.randn(hidden_size, 1) * 0.1
self.W2 = np.random.randn(output_size, hidden_size) * 0.1
self.b2 = np.random.randn(output_size, 1) * 0.1
self.learning_rate = learning_rate
def forward(self, X):
"""Forward propagation"""
# Layer 1
self.Z1 = np.dot(self.W1, X) + self.b1
self.A1 = sigmoid(self.Z1)
# Layer 2
self.Z2 = np.dot(self.W2, self.A1) + self.b2
self.A2 = sigmoid(self.Z2)
return self.A2
def backward(self, X, y, y_pred):
"""Backpropagation"""
m = X.shape[1] # Number of examples
# Output layer gradients
dA2 = mse_loss_derivative(y, y_pred)
dZ2 = dA2 * sigmoid_derivative(self.Z2)
dW2 = np.dot(dZ2, self.A1.T) / m
db2 = np.sum(dZ2, axis=1, keepdims=True) / m
# Hidden layer gradients
dA1 = np.dot(self.W2.T, dZ2)
dZ1 = dA1 * sigmoid_derivative(self.Z1)
dW1 = np.dot(dZ1, X.T) / m
db1 = np.sum(dZ1, axis=1, keepdims=True) / m
# Update weights
self.W2 -= self.learning_rate * dW2
self.b2 -= self.learning_rate * db2
self.W1 -= self.learning_rate * dW1
self.b1 -= self.learning_rate * db1
def train(self, X, y, epochs=1000):
"""Training loop"""
for epoch in range(epochs):
# Forward pass
y_pred = self.forward(X)
# Compute loss
loss = mse_loss(y, y_pred)
# Backward pass
self.backward(X, y, y_pred)
# Print progress
if epoch % 100 == 0:
print(f"Epoch {epoch}, Loss: {loss:.4f}")
# Example usage
X = np.array([[0.5], [0.8]])
y = np.array([[1]])
network = TwoLayerNetwork(input_size=2, hidden_size=2, output_size=1)
network.train(X, y, epochs=1000)
# Test
prediction = network.forward(X)
print(f"Final prediction: {prediction[0][0]:.4f}")Deep Network (L layers)
class DeepNetwork:
def __init__(self, layer_sizes, learning_rate=0.01):
"""
layer_sizes: list of layer sizes (including input and output)
Example: [2, 4, 3, 1] = 2 inputs, 2 hidden layers (4, 3 neurons), 1 output
"""
self.L = len(layer_sizes) - 1 # Number of layers (excluding input)
self.learning_rate = learning_rate
self.parameters = {}
# Initialize weights and biases
for l in range(1, self.L + 1):
self.parameters[f'W{l}'] = np.random.randn(
layer_sizes[l], layer_sizes[l-1]
) * 0.01
self.parameters[f'b{l}'] = np.zeros((layer_sizes[l], 1))
def forward(self, X):
"""Forward propagation"""
self.cache = {'A0': X}
A = X
for l in range(1, self.L + 1):
W = self.parameters[f'W{l}']
b = self.parameters[f'b{l}']
Z = np.dot(W, A) + b
A = sigmoid(Z)
self.cache[f'Z{l}'] = Z
self.cache[f'A{l}'] = A
return A
def backward(self, X, y, y_pred):
"""Backpropagation"""
m = X.shape[1]
grads = {}
# Output layer
dA = mse_loss_derivative(y, y_pred)
# Backward through layers
for l in range(self.L, 0, -1):
Z = self.cache[f'Z{l}']
A_prev = self.cache[f'A{l-1}']
dZ = dA * sigmoid_derivative(Z)
dW = np.dot(dZ, A_prev.T) / m
db = np.sum(dZ, axis=1, keepdims=True) / m
if l > 1:
W = self.parameters[f'W{l}']
dA = np.dot(W.T, dZ)
grads[f'dW{l}'] = dW
grads[f'db{l}'] = db
# Update parameters
for l in range(1, self.L + 1):
self.parameters[f'W{l}'] -= self.learning_rate * grads[f'dW{l}']
self.parameters[f'b{l}'] -= self.learning_rate * grads[f'db{l}']Key Insights and Intuitions
Insight 1: Error Attribution
Backpropagation attributes error to each weight:
- Weights that caused large errors get large gradients
- Weights that contributed little get small gradients
- Update magnitude proportional to contribution to error
Analogy: Team project feedback
- Members who contributed to mistakes get more corrective feedback
- Everyone adjusts based on their specific contribution
Insight 2: Chain Rule Enables Decomposition
Complex derivative broken into simple pieces:
- ∂Loss/∂W₁ = (∂Loss/∂A₃) × (∂A₃/∂Z₃) × (∂Z₃/∂A₂) × (∂A₂/∂Z₂) × (∂Z₂/∂A₁) × (∂A₁/∂Z₁) × (∂Z₁/∂W₁)
Each piece is simple to calculate Multiply them together → final gradient
Insight 3: Reuse of Computations
Efficient: Calculate gradients layer by layer
- Compute gradient for layer L
- Use it to compute gradient for layer L-1
- Reuse intermediate results
Without backprop: Would need to compute each gradient independently (exponentially slower)
Insight 4: Local Information Sufficient
Each neuron only needs:
- Its own activation and gradient
- Gradients from next layer
- Activations from previous layer
Doesn’t need global view of entire network
Insight 5: Gradient Magnitudes Matter
Small gradients:
- Small updates
- Slow learning
- Can indicate vanishing gradient problem
Large gradients:
- Large updates
- Fast learning (or instability)
- Can indicate exploding gradient problem
Ideal: Moderate, consistent gradients throughout network
Common Problems and Solutions
Problem 1: Vanishing Gradients
Symptom: Gradients become extremely small in early layers
Cause:
- Sigmoid/tanh saturate (flat regions)
- Gradients multiply through layers
- Product of many small numbers → vanishing
Example:
Sigmoid derivative max = 0.25
10 layers: 0.25^10 ≈ 0.000001
Gradient vanishes!Solutions:
- Use ReLU activation (gradient = 1 for positive values)
- Careful weight initialization (Xavier, He)
- Batch normalization
- Residual connections (skip connections)
- Gradient clipping
Problem 2: Exploding Gradients
Symptom: Gradients become extremely large
Cause:
- Large weights
- Deep networks
- Activations without bounds (ReLU)
- Gradients multiply → explosion
Solutions:
- Gradient clipping (cap maximum gradient)
- Better weight initialization
- Lower learning rate
- Batch normalization
Problem 3: Dead Neurons
Symptom: Neurons always output 0 (ReLU)
Cause:
- Large negative weighted sum
- ReLU outputs 0
- Gradient = 0
- Weight never updates
Solutions:
- Use Leaky ReLU
- Proper initialization
- Lower learning rate
- Monitor neuron activations
Problem 4: Slow Convergence
Symptom: Loss decreases very slowly
Causes:
- Learning rate too small
- Poor initialization
- Plateaus in loss landscape
Solutions:
- Increase learning rate
- Use adaptive optimizers (Adam, RMSprop)
- Better initialization
- Momentum-based methods
Optimizers: Improving Backpropagation
Basic backpropagation uses simple gradient descent. Modern optimizers enhance it:
Momentum
Idea: Accumulate velocity from past gradients
v = β × v + (1 - β) × gradient
W = W - α × vBenefit: Smooths updates, accelerates in consistent directions
RMSprop
Idea: Adapt learning rate per parameter based on recent gradients
s = β × s + (1 - β) × gradient²
W = W - α × gradient / √(s + ε)Benefit: Different learning rates for different parameters
Adam (Adaptive Moment Estimation)
Idea: Combines momentum and RMSprop
m = β₁ × m + (1 - β₁) × gradient # Momentum
v = β₂ × v + (1 - β₂) × gradient² # RMSprop
W = W - α × m / √(v + ε)Benefit: Generally works well, widely used default
Comparison: Backpropagation vs. Alternatives
| Aspect | Backpropagation | Numerical Gradient | Evolution Strategies |
|---|---|---|---|
| Method | Analytical gradients | Finite differences | Population-based |
| Speed | Very fast | Very slow | Slow |
| Accuracy | Exact | Approximate | No gradients |
| Memory | Moderate (store activations) | Low | Low |
| Parallelization | Layer-wise | Fully parallel | Fully parallel |
| Use Case | Standard for NN training | Gradient checking | Specific problems |
| Scalability | Excellent | Poor | Limited |
Gradient Checking: Verifying Backpropagation
Purpose: Verify backpropagation implementation is correct
Method: Compare analytical gradients (from backprop) to numerical gradients
Numerical Gradient:
∂Loss/∂w ≈ (Loss(w + ε) - Loss(w - ε)) / (2ε)
Where ε is small (e.g., 10^-7)Process:
def gradient_check(parameters, gradients, X, y, epsilon=1e-7):
"""Check if backprop gradients are correct"""
for param_name in parameters:
param = parameters[param_name]
grad = gradients[f'd{param_name}']
# Compute numerical gradient
numerical_grad = np.zeros_like(param)
it = np.nditer(param, flags=['multi_index'])
while not it.finished:
ix = it.multi_index
old_value = param[ix]
# f(w + epsilon)
param[ix] = old_value + epsilon
loss_plus = compute_loss(X, y, parameters)
# f(w - epsilon)
param[ix] = old_value - epsilon
loss_minus = compute_loss(X, y, parameters)
# Numerical gradient
numerical_grad[ix] = (loss_plus - loss_minus) / (2 * epsilon)
param[ix] = old_value
it.iternext()
# Compare
diff = np.linalg.norm(grad - numerical_grad)
print(f"{param_name}: difference = {diff}")
if diff < 1e-7:
print("✓ Gradient check passed")
else:
print("✗ Gradient check failed")When to Use:
- Implementing backprop from scratch
- Debugging gradient calculations
- Testing custom layers/operations
Note: Disable for training (too slow)
Practical Tips for Backpropagation
1. Always Normalize Inputs
X = (X - X.mean()) / X.std()Why: Helps gradients flow evenly
2. Use Proper Weight Initialization
# Xavier initialization (sigmoid/tanh)
W = np.random.randn(n_out, n_in) * np.sqrt(1 / n_in)
# He initialization (ReLU)
W = np.random.randn(n_out, n_in) * np.sqrt(2 / n_in)Why: Prevents gradients from vanishing/exploding initially
3. Start with Small Learning Rates
learning_rate = 0.01 # Start here
# Increase if learning too slow
# Decrease if unstableWhy: Large learning rates can cause divergence
4. Monitor Gradients
# During training, check gradient norms
grad_norm = np.linalg.norm(gradients)
if grad_norm > 10:
print("Warning: Large gradients")Why: Detect exploding/vanishing gradients early
5. Use Batch Normalization
# Normalize activations between layers
A = batch_normalize(Z)Why: Stabilizes gradients, enables faster learning
Conclusion: The Engine of Deep Learning
Backpropagation is the algorithm that makes deep learning possible. By efficiently computing gradients through the chain rule, it enables networks with millions or billions of parameters to learn from data. Every time you train a neural network—whether classifying images, translating text, or playing games—backpropagation is the engine driving improvement.
Understanding backpropagation means grasping:
The mathematics: Chain rule decomposing complex derivatives into manageable pieces, calculated efficiently layer by layer.
The mechanics: Forward pass computes predictions and caches values, backward pass computes gradients using cached values, weights update in direction that reduces error.
The challenges: Vanishing and exploding gradients, dead neurons, slow convergence—and solutions like ReLU, proper initialization, and adaptive optimizers.
The elegance: A simple algorithm—calculate gradients backward, update weights forward—that scales to the deepest networks and most complex problems.
While backpropagation’s mathematical details can seem intimidating, its core idea is intuitive: determine how much each weight contributed to error, then adjust weights to reduce that contribution. This simple principle, implemented efficiently through calculus, enables the learning that powers modern AI.
As you work with neural networks, remember that backpropagation isn’t just theory—it’s the actual mechanism by which networks improve. Understanding it helps you debug training problems, choose appropriate architectures, set hyperparameters wisely, and ultimately build better models.
The next time you see a network’s loss decreasing during training, you’ll know exactly what’s happening: backpropagation calculating gradients, gradient descent updating weights, the network incrementally improving its ability to map inputs to outputs. That’s the power of backpropagation—the algorithm that learns.