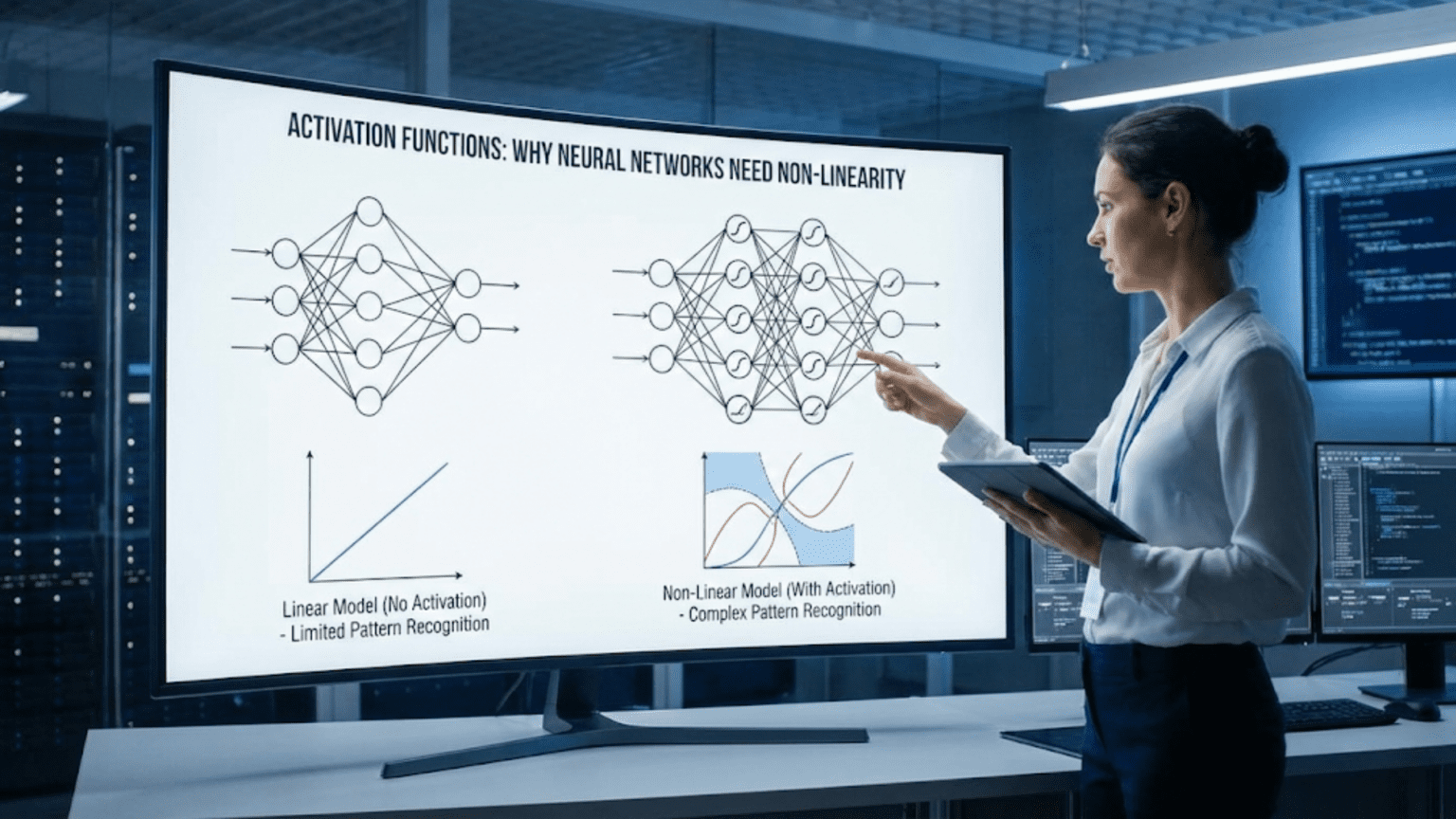
Activation functions introduce non-linearity into neural networks by transforming the weighted sum of inputs through mathematical functions like sigmoid, tanh, or ReLU. Without activation functions, neural networks would be equivalent to linear regression regardless of depth, unable to learn complex patterns. Non-linearity enables networks to approximate any function, create curved decision boundaries, learn hierarchical features, and solve problems like image recognition and language understanding that require capturing intricate relationships in data.
Introduction: The Secret to Neural Network Power
Imagine building a tower from blocks, but every block you add must be perfectly aligned with the ones below—no angles, no curves, just straight stacks. No matter how many blocks you add, you can only build straight vertical structures. This is what neural networks without activation functions are like: no matter how many layers you add, they can only learn linear relationships.
Activation functions are the simple yet profound ingredient that transforms neural networks from glorified linear models into universal function approximators capable of learning virtually any pattern. A single mathematical operation applied to each neuron’s output—taking a number and transforming it through a function like sigmoid, ReLU, or tanh—fundamentally changes what networks can learn.
Without activation functions, a 100-layer deep neural network is mathematically equivalent to a single-layer linear model. With activation functions, that same network can recognize faces, understand language, play chess at superhuman levels, and generate creative content. The difference is non-linearity: the ability to learn curved, complex decision boundaries rather than just straight lines.
Understanding activation functions is crucial for anyone working with neural networks. They determine how information flows through networks, affect training speed and stability, influence what patterns can be learned, and impact whether networks can even train successfully. Choosing the wrong activation function can make training impossible; choosing the right one enables remarkable performance.
This comprehensive guide explores activation functions in depth. You’ll learn why neural networks need non-linearity, how activation functions work, the properties of different functions, when to use each type, common problems they solve or cause, and practical guidance for selecting activations for your networks.
The Problem: Why Linear is Limited
To appreciate activation functions, we must first understand the limitation they solve.
Neural Networks Without Activation Functions
Consider a simple neural network with two layers, no activation functions:
Layer 1:
h = W₁x + b₁
Where:
- x = input
- W₁ = weights
- b₁ = bias
- h = hidden layer outputLayer 2:
y = W₂h + b₂Combined:
y = W₂(W₁x + b₁) + b₂
y = W₂W₁x + W₂b₁ + b₂
y = Wx + b (where W = W₂W₁, b = W₂b₁ + b₂)Result: This is just a linear transformation—equivalent to simple linear regression!
The Collapse: Multiple layers without activation functions collapse into a single linear layer.
Why This is Problematic
Linear Models Can Only Learn Linear Relationships:
Example: XOR Problem
x₁ x₂ output
0 0 0
0 1 1
1 0 1
1 1 0No straight line separates the 1s from 0s. Linear model cannot solve this.
Real-World Implications:
- Cannot recognize images (requires detecting curves, edges, complex shapes)
- Cannot understand language (requires hierarchical, non-linear relationships)
- Cannot play games strategically (requires complex decision-making)
- Limited to problems with linear relationships
The Fundamental Limitation:
Linear transformations of linear transformations = still linear
f(g(x)) is linear if both f and g are linear
No matter how many layers, still just computing:
y = Wx + bThe Solution: Introducing Non-Linearity
Activation functions break the linearity by applying non-linear transformations.
How Activation Functions Work
In Each Neuron:
Step 1: Weighted Sum (linear)
z = w₁x₁ + w₂x₂ + ... + wₙxₙ + b
z = Wx + bStep 2: Activation Function (non-linear)
a = f(z)
Where f is the activation function (e.g., ReLU, sigmoid, tanh)Network with Activations:
Layer 1: h = f₁(W₁x + b₁)
Layer 2: y = f₂(W₂h + b₂)
Combined: y = f₂(W₂ × f₁(W₁x + b₁) + b₂)Key Difference: Because of f₁ and f₂, this is NOT a linear transformation of x!
Why Non-Linearity Matters
1. Enables Complex Decision Boundaries
Linear (no activation):
Decision boundary: straight line/plane
Can separate: linearly separable classes onlyNon-linear (with activation):
Decision boundary: curved, complex shapes
Can separate: arbitrary patterns2. Enables Hierarchical Learning
Example: Image Recognition
Layer 1 (with activation): Learns edges, textures
Layer 2 (with activation): Combines edges into shapes
Layer 3 (with activation): Combines shapes into objects
Output: Classification
Without activation: All layers collapse to one linear layer
Cannot build hierarchy3. Universal Function Approximation
Universal Approximation Theorem: A neural network with one hidden layer and non-linear activation can approximate any continuous function (given enough neurons).
Requirement: Non-linear activation function!
- With activation: Can approximate any function
- Without activation: Can only approximate linear functions
Popular Activation Functions
Different activation functions have different properties and use cases.
1. Sigmoid (Logistic Function)
Formula:
σ(z) = 1 / (1 + e^(-z))Output Range: (0, 1)
Shape: S-shaped curve
Properties:
- Smooth, differentiable
- Output interpretable as probability
- Saturates at extremes (flat regions)
Derivative:
σ'(z) = σ(z) × (1 - σ(z))Visual:
Output
1.0 │ ╱‾‾‾‾
│ ╱
0.5 │ ╱
│ ╱
0.0 │╱___________z
-5 0 5Advantages:
- Smooth gradient
- Output in (0,1) – useful for probabilities
- Well-understood, classic choice
Disadvantages:
- Vanishing Gradient Problem:
- For large |z|, gradient near zero
- Makes learning slow in deep networks
- Affects early layers especially
- Not Zero-Centered:
- Outputs always positive
- Can slow convergence
- Computationally Expensive:
- Exponential calculation
When to Use:
- Output layer for binary classification (need probabilities)
- Shallow networks
- Not recommended for hidden layers in deep networks
Example:
import numpy as np
def sigmoid(z):
return 1 / (1 + np.exp(-z))
z = np.array([-2, -1, 0, 1, 2])
a = sigmoid(z)
# Output: [0.119, 0.269, 0.5, 0.731, 0.881]2. Tanh (Hyperbolic Tangent)
Formula:
tanh(z) = (e^z - e^(-z)) / (e^z + e^(-z))
= 2σ(2z) - 1Output Range: (-1, 1)
Shape: S-shaped, similar to sigmoid but centered at 0
Properties:
- Smooth, differentiable
- Zero-centered (unlike sigmoid)
- Still saturates at extremes
Derivative:
tanh'(z) = 1 - tanh²(z)
Visual:
Output
1.0 │ ╱‾‾‾‾
│ ╱
0.0 │ ╱
│╱
-1.0 │___________z
-5 0 5Advantages:
- Zero-centered (better than sigmoid)
- Stronger gradients than sigmoid
- Smooth gradient
Disadvantages:
- Still suffers from vanishing gradients
- Computationally expensive (exponentials)
When to Use:
- Hidden layers (better than sigmoid)
- Recurrent Neural Networks (LSTM, GRU gates)
- When need zero-centered outputs
Example:
def tanh(z):
return np.tanh(z)
z = np.array([-2, -1, 0, 1, 2])
a = tanh(z)
# Output: [-0.964, -0.762, 0, 0.762, 0.964]3. ReLU (Rectified Linear Unit)
Formula:
ReLU(z) = max(0, z) = {z if z > 0
{0 if z ≤ 0Output Range: [0, ∞)
Shape: Linear for positive values, zero for negative
Properties:
- Very simple computation
- Non-linear (despite being piecewise linear!)
- Not differentiable at z=0 (but not a problem in practice)
Derivative:
ReLU'(z) = {1 if z > 0
{0 if z ≤ 0
(undefined at z=0, use 0 or 1 in practice)Visual:
Output
│ ╱
│ ╱
│╱
0 ──┼────────z
0Advantages:
- Computationally Efficient: Just max(0, z)
- No Vanishing Gradient (for positive values)
- Sparse Activation: Many neurons output 0
- Faster Convergence: Typically 6x faster than sigmoid/tanh
- Biologically Plausible: Similar to neuron firing rates
Disadvantages:
- Dying ReLU Problem:
- Neurons can get stuck outputting 0
- If z always negative, gradient always 0
- Neuron never updates (dies)
- Not Zero-Centered: Only outputs ≥ 0
- Unbounded: Output can grow very large
When to Use:
- Default choice for hidden layers
- Convolutional Neural Networks
- Most deep networks
- When training speed important
Example:
def relu(z):
return np.maximum(0, z)
z = np.array([-2, -1, 0, 1, 2])
a = relu(z)
# Output: [0, 0, 0, 1, 2]4. Leaky ReLU
Formula:
Leaky ReLU(z) = {z if z > 0
{αz if z ≤ 0
Where α is a small constant (typically 0.01)Output Range: (-∞, ∞)
Visual:
Output
│ ╱
│ ╱
╱ │╱
────┼────────z
0
(small slope for negative z)Advantages:
- Fixes Dying ReLU: Small gradient for negative values
- Still computationally efficient
- Better gradient flow
Disadvantages:
- Extra hyperparameter (α)
- Inconsistent benefits across problems
Variants:
- Parametric ReLU (PReLU): α is learned during training
- Randomized Rleaky ReLU: α is random during training
When to Use:
- When experiencing dying ReLU problem
- Alternative to standard ReLU
Example:
def leaky_relu(z, alpha=0.01):
return np.where(z > 0, z, alpha * z)
z = np.array([-2, -1, 0, 1, 2])
a = leaky_relu(z)
# Output: [-0.02, -0.01, 0, 1, 2]5. ELU (Exponential Linear Unit)
Formula:
ELU(z) = {z if z > 0
{α(e^z - 1) if z ≤ 0Output Range: (-α, ∞)
Properties:
- Smooth everywhere
- Negative values push mean activation closer to zero
- Reduces bias shift
Advantages:
- No dying ReLU
- Smooth, better gradient flow
- Faster convergence than ReLU in some cases
Disadvantages:
- Exponential computation (slower than ReLU)
- Extra hyperparameter (α)
When to Use:
- When need smoother activation than ReLU
- When dying ReLU is a problem
6. Softmax
Formula (for vector output):
softmax(zᵢ) = e^zᵢ / Σⱼ(e^zⱼ)Output Range: (0, 1) for each element, sum = 1
Properties:
- Converts vector to probability distribution
- All outputs between 0 and 1
- All outputs sum to 1
When to Use:
- Output layer for multi-class classification
- When need probability distribution over classes
Example:
def softmax(z):
exp_z = np.exp(z - np.max(z)) # Subtract max for numerical stability
return exp_z / np.sum(exp_z)
z = np.array([2.0, 1.0, 0.1])
a = softmax(z)
# Output: [0.659, 0.242, 0.099] (sums to 1.0)7. Swish (SiLU)
Formula:
Swish(z) = z × σ(z) = z / (1 + e^(-z))Properties:
- Smooth, non-monotonic
- Self-gated (z multiplied by sigmoid of itself)
- Discovered by Google through neural architecture search
Advantages:
- Can outperform ReLU in deep networks
- Smooth gradient
Disadvantages:
- Computationally more expensive than ReLU
When to Use:
- Deep networks where squeeze out extra performance
Comparison of Activation Functions
| Function | Formula | Range | Advantages | Disadvantages | Best For |
|---|---|---|---|---|---|
| Sigmoid | 1/(1+e^(-z)) | (0,1) | Smooth, probability output | Vanishing gradient, not zero-centered | Output layer (binary) |
| Tanh | (e^z-e^(-z))/(e^z+e^(-z)) | (-1,1) | Zero-centered, smooth | Vanishing gradient | RNN gates, hidden layers |
| ReLU | max(0,z) | [0,∞) | Fast, no vanishing gradient | Dying ReLU, unbounded | Default for hidden layers |
| Leaky ReLU | max(αz,z) | (-∞,∞) | Fixes dying ReLU | Extra hyperparameter | Alternative to ReLU |
| ELU | z or α(e^z-1) | (-α,∞) | Smooth, faster convergence | Exponential computation | When need smooth activation |
| Softmax | e^zᵢ/Σe^zⱼ | (0,1), sum=1 | Probability distribution | Only for output | Multi-class output layer |
| Swish | z×σ(z) | (-∞,∞) | Can outperform ReLU | Computationally expensive | Deep networks |
Key Problems Activation Functions Solve (or Cause)
Problem 1: Vanishing Gradient
Issue: Gradients become extremely small in deep networks
Cause:
- Sigmoid/tanh saturate (flat regions)
- Gradient near zero in saturated regions
- Multiplying many small gradients → tiny gradients
- Early layers barely update
Visual:
Sigmoid gradient:
│ ╱‾╲
0.25│ ╱ ╲
│╱_____╲___
z
Maximum gradient = 0.25
In 10 layers: 0.25^10 ≈ 0.000001 (vanishing!)Solution: Use ReLU-family activations
- ReLU gradient = 1 for positive values
- No saturation for positive inputs
- Gradient doesn’t vanish
Problem 2: Dying ReLU
Issue: ReLU neurons can “die” (permanently output 0)
Cause:
- If weighted sum always negative
- ReLU always outputs 0
- Gradient always 0
- Neuron never updates
Example:
Neuron with large negative bias
z = wx + b (always negative)
ReLU(z) = 0 (always)
Gradient = 0 (always)
Weight never updates → neuron deadSolutions:
- Use Leaky ReLU (small gradient for negative)
- Careful initialization
- Lower learning rate
- Batch normalization
Problem 3: Exploding Gradients
Issue: Gradients become extremely large
Cause:
- Unbounded activations (ReLU)
- Large weights
- Deep networks
- Gradients multiply → explosion
Solutions:
- Gradient clipping
- Proper weight initialization
- Batch normalization
- Use activations with bounded outputs (when appropriate)
Problem 4: Slow Convergence
Issue: Training takes very long
Causes:
- Wrong activation choice
- Vanishing gradients
- Non-zero-centered activations
Solutions:
- Use ReLU for faster convergence
- Zero-centered activations (tanh better than sigmoid)
- Proper initialization
- Batch normalization
Practical Guidelines: Choosing Activation Functions
General Rules
Hidden Layers:
First choice: ReLU
- Fast, effective, widely used
- Default recommendation
If dying ReLU problem: Leaky ReLU or ELU
- Small gradient for negative values
- Prevents dead neurons
For RNNs: Tanh (in gates)
- Zero-centered
- Bounded output
- Traditional choice for LSTM/GRUOutput Layer:
Binary classification: Sigmoid
- Outputs probability (0-1)
Multi-class classification: Softmax
- Probability distribution over classes
Regression: Linear (no activation) or ReLU
- Linear: Can output any value
- ReLU: If output should be non-negativeArchitecture-Specific Guidelines
Convolutional Neural Networks (CNNs):
- Hidden layers: ReLU
- Output: Softmax (classification) or Linear (regression)
Recurrent Neural Networks (RNNs):
- Gates (LSTM/GRU): Sigmoid and Tanh
- Output: Depends on task
Deep Networks (10+ layers):
- ReLU or variants
- Avoid sigmoid/tanh (vanishing gradient)
- Consider batch normalization
Shallow Networks (1-3 layers):
- More flexible, sigmoid/tanh acceptable
- ReLU still good choice
Problem-Specific Guidelines
Image Classification:
- Hidden: ReLU
- Output: Softmax
Image Regression (e.g., age prediction):
- Hidden: ReLU
- Output: Linear or ReLU
Time Series Forecasting:
- LSTM/GRU with tanh and sigmoid
- Output: Linear
Reinforcement Learning:
- Hidden: ReLU
- Output: Depends on action space
Implementation Examples
Using Different Activations in Keras/TensorFlow
from tensorflow.keras import Sequential, layers
# ReLU activation
model = Sequential([
layers.Dense(128, activation='relu', input_shape=(784,)),
layers.Dense(64, activation='relu'),
layers.Dense(10, activation='softmax') # Output layer
])
# Explicitly specifying activation layers
model = Sequential([
layers.Dense(128, input_shape=(784,)),
layers.Activation('relu'),
layers.Dense(64),
layers.Activation('relu'),
layers.Dense(10),
layers.Activation('softmax')
])
# Using different activations
model = Sequential([
layers.Dense(128, activation='tanh'), # Tanh
layers.Dense(64, activation='elu'), # ELU
layers.Dense(32, activation='selu'), # SELU
layers.Dense(10, activation='softmax')
])
# Leaky ReLU (special case)
from tensorflow.keras.layers import LeakyReLU
model = Sequential([
layers.Dense(128),
LeakyReLU(alpha=0.01),
layers.Dense(64),
LeakyReLU(alpha=0.01),
layers.Dense(10, activation='softmax')
])PyTorch Implementation
import torch.nn as nn
class Network(nn.Module):
def __init__(self):
super(Network, self).__init__()
self.fc1 = nn.Linear(784, 128)
self.fc2 = nn.Linear(128, 64)
self.fc3 = nn.Linear(64, 10)
# Activation functions
self.relu = nn.ReLU()
self.sigmoid = nn.Sigmoid()
self.tanh = nn.Tanh()
self.softmax = nn.Softmax(dim=1)
def forward(self, x):
x = self.relu(self.fc1(x)) # Hidden layer 1 with ReLU
x = self.relu(self.fc2(x)) # Hidden layer 2 with ReLU
x = self.softmax(self.fc3(x)) # Output with softmax
return x
# Alternative: inline activations
class SimpleNetwork(nn.Module):
def __init__(self):
super(SimpleNetwork, self).__init__()
self.layers = nn.Sequential(
nn.Linear(784, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 10),
nn.Softmax(dim=1)
)
def forward(self, x):
return self.layers(x)Custom Activation Function
# NumPy implementation
def custom_activation(z):
"""Custom activation: z^2 for z>0, 0 otherwise"""
return np.where(z > 0, z**2, 0)
# TensorFlow custom activation
from tensorflow.keras import backend as K
def custom_activation_keras(z):
return K.maximum(z**2, 0)
# Use in model
model = Sequential([
layers.Dense(128),
layers.Lambda(custom_activation_keras),
layers.Dense(10, activation='softmax')
])Historical Evolution of Activation Functions
1950s-1980s: Sigmoid and Tanh
- Classic choices
- Inspired by biological neurons
- Dominated early neural networks
1990s-2000s: Limitations Recognized
- Vanishing gradient problem identified
- Hindered deep network training
- Led to “AI Winter” for neural networks
2011: ReLU Revolution
- Krizhevsky et al. (AlexNet) popularized ReLU
- Enabled training deeper networks
- Faster convergence
- Became default choice
2015-Present: ReLU Variants
- Leaky ReLU, PReLU, ELU
- Addressing dying ReLU
- Searching for better alternatives
Recent: Neural Architecture Search
- Swish discovered by automated search
- Mish, GELU developed
- Ongoing research for optimal activations
The Future of Activation Functions
Research Directions:
Learned Activations:
- Activation function learned during training
- Adaptive to specific problems
- Examples: PReLU, Maxout
Self-Normalizing:
- SELU (Scaled ELU)
- Induces self-normalization
- May reduce need for batch normalization
Smooth Approximations:
- Softplus: Smooth approximation of ReLU
- GELU: Smooth, used in transformers (BERT, GPT)
Task-Specific:
- Different activations for different domains
- Computer vision: ReLU variants
- NLP: GELU gaining popularity
- Customized for specific architectures
Conclusion: The Power of Non-Linearity
Activation functions are deceptively simple yet profoundly important. By introducing non-linearity through basic mathematical operations—taking a max with zero, computing an exponential, or multiplying by a sigmoid—they transform neural networks from limited linear models into powerful universal function approximators.
The evolution from sigmoid to ReLU exemplifies how seemingly small changes can enable dramatic progress. ReLU’s simple formula—max(0, z)—solved the vanishing gradient problem that plagued deep learning for decades, enabling the deep networks that power modern AI.
Understanding activation functions requires grasping several key concepts:
Non-linearity is essential: Without it, neural networks collapse to linear models regardless of depth.
Different functions have different properties: Sigmoid outputs probabilities but suffers from vanishing gradients. ReLU trains fast but can die. Tanh is zero-centered but computationally expensive.
Choose based on position and task: ReLU for hidden layers, softmax for multi-class output, sigmoid for binary output.
Be aware of problems: Vanishing gradients, dying ReLU, exploding gradients—understanding these helps debug training issues.
As you build neural networks, treat activation function selection thoughtfully. The default ReLU works well for most hidden layers, but understanding alternatives enables better choices for specific situations. Experiment, monitor training, and adapt based on results.
The humble activation function—a simple non-linear transformation applied billions of times during training—is what allows neural networks to learn the complex patterns that make modern AI possible. Master activation functions, and you’ve mastered a fundamental building block of deep learning.