Introduction
After learning NumPy basics including array creation, indexing, and simple operations, you possess foundation for numerical computing in Python. However, real data science work requires more sophisticated array manipulation: combining datasets from different sources, reshaping data for machine learning algorithms, performing matrix operations for linear models, and applying complex transformations efficiently. NumPy provides powerful operations for these tasks that, once mastered, enable you to handle virtually any array manipulation challenge you encounter in practice.
The operations covered in this guide separate casual NumPy users from those who wield it expertly. Broadcasting lets you perform operations on arrays with different shapes without manual reshaping or looping. Stacking and concatenation combine arrays along various dimensions, essential when assembling datasets from multiple sources. Advanced indexing techniques enable complex selections that would require convoluted loops otherwise. Linear algebra operations provide matrix multiplication, decompositions, and solvers needed for statistical models and machine learning. Understanding these operations deeply transforms your data manipulation from awkward, slow code into elegant, fast expressions.
What makes these operations particularly valuable is how they compose together. You might filter an array using fancy indexing, reshape the result for a machine learning model, normalize using broadcasting, then apply matrix operations for predictions. Each operation works seamlessly with others because they all manipulate the same ndarray objects using consistent interfaces. This composability enables building complex data processing pipelines from simple, understandable operations. Moreover, these NumPy patterns transfer directly to pandas, TensorFlow, PyTorch, and other libraries built on NumPy’s array concepts.
This comprehensive guide explores essential NumPy operations that appear constantly in data science work. You will learn how broadcasting extends operations to arrays of different shapes, how to combine arrays using concatenation, stacking, and splitting, how to perform advanced selections using fancy indexing and where clauses, how to sort and search arrays efficiently, how to apply universal functions and custom operations, and how to perform linear algebra operations for mathematical modeling. You will also discover memory efficiency considerations and best practices for writing fast, readable NumPy code. By the end, you will recognize patterns for solving array manipulation problems and write code that leverages NumPy’s full power.
Broadcasting: Operations on Arrays of Different Shapes
Broadcasting represents one of NumPy’s most powerful features, enabling operations between arrays with different but compatible shapes without explicit duplication of data. Understanding broadcasting mechanics and rules prevents confusion and enables elegant solutions to common problems.
The simplest broadcasting case involves operations between an array and a scalar:
import numpy as np
arr = np.array([1, 2, 3, 4, 5])
result = arr + 10 # Scalar broadcasts to match array shape
print(result) # [11 12 13 14 15]
# Works with any operation
result = arr * 2
print(result) # [ 2 4 6 8 10]The scalar 10 broadcasts to shape (5,) matching the array, as if it were [10, 10, 10, 10, 10], but without actually creating that array in memory.
Broadcasting works with arrays of different dimensions:
# 2D array
matrix = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# 1D array
row = np.array([10, 20, 30])
# Add row to each row of matrix
result = matrix + row
print(result)
# [[11 22 33]
# [14 25 36]
# [17 28 39]]The 1D array broadcasts across rows of the 2D array. Visually, it extends to:
[[10 20 30] [[1 2 3] [[11 22 33]
[10 20 30] + [4 5 6] = [14 25 36]
[10 20 30]] [7 8 9]] [17 28 39]]Broadcasting rules determine when operations are valid:
- Compare array shapes element-wise from right to left
- Dimensions are compatible if they are equal or one of them is 1
- Missing dimensions are treated as having size 1
Examples:
# Shape (3, 4) and (4,)
# (3, 4) + (4,) -> Compatible
# Broadcasts (4,) to (1, 4) to match
# Shape (3, 1) and (3, 4)
# (3, 1) + (3, 4) -> Compatible
# Broadcasts (3, 1) to (3, 4)
# Shape (3, 4) and (3,)
# (3, 4) + (3,) -> NOT compatible
# (3,) would broadcast to (1, 3), incompatible with (3, 4)Add newaxis to control broadcasting:
# Column vector
col = np.array([10, 20, 30])
print(col.shape) # (3,)
# Add new axis to make it (3, 1)
col = col[:, np.newaxis]
print(col.shape) # (3, 1)
# Now broadcasts across columns
matrix = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
result = matrix + col
print(result)
# [[11 12 13]
# [24 25 26]
# [37 38 39]]Common broadcasting patterns in data science:
# Normalize each row by its mean
data = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
row_means = data.mean(axis=1, keepdims=True) # Shape (3, 1)
normalized = data - row_means
print(normalized)
# [[-1. 0. 1.]
# [-1. 0. 1.]
# [-1. 0. 1.]]
# Standardize each column
col_means = data.mean(axis=0) # Shape (3,)
col_stds = data.std(axis=0) # Shape (3,)
standardized = (data - col_means) / col_stds
print(standardized)Broadcasting enables distance calculations:
# Calculate Euclidean distances between all pairs of points
points = np.array([[1, 2],
[3, 4],
[5, 6]])
# Reshape for broadcasting: (3, 1, 2) - (1, 3, 2)
distances = np.sqrt(((points[:, np.newaxis] - points) ** 2).sum(axis=2))
print(distances)Combining Arrays: Concatenate, Stack, and Split
Combining multiple arrays into single arrays or splitting arrays into multiple pieces appears constantly in data processing workflows.
Concatenate arrays along existing axes:
arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
# Concatenate along axis 0 (default)
result = np.concatenate([arr1, arr2])
print(result) # [1 2 3 4 5 6]
# Works with multiple arrays
arr3 = np.array([7, 8, 9])
result = np.concatenate([arr1, arr2, arr3])
print(result) # [1 2 3 4 5 6 7 8 9]Concatenate 2D arrays:
mat1 = np.array([[1, 2],
[3, 4]])
mat2 = np.array([[5, 6],
[7, 8]])
# Concatenate vertically (axis 0)
result = np.concatenate([mat1, mat2], axis=0)
print(result)
# [[1 2]
# [3 4]
# [5 6]
# [7 8]]
# Concatenate horizontally (axis 1)
result = np.concatenate([mat1, mat2], axis=1)
print(result)
# [[1 2 5 6]
# [3 4 7 8]]Convenience functions for common concatenations:
arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
# Vertical stack (vstack) - stack arrays as rows
result = np.vstack([arr1, arr2])
print(result)
# [[1 2 3]
# [4 5 6]]
# Horizontal stack (hstack) - concatenate horizontally
result = np.hstack([arr1, arr2])
print(result) # [1 2 3 4 5 6]
# Column stack (column_stack) - stack 1D arrays as columns
result = np.column_stack([arr1, arr2])
print(result)
# [[1 4]
# [2 5]
# [3 6]]Stack arrays along new axis:
arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
# Stack along new axis 0
result = np.stack([arr1, arr2], axis=0)
print(result)
# [[1 2 3]
# [4 5 6]]
print(result.shape) # (2, 3)
# Stack along new axis 1
result = np.stack([arr1, arr2], axis=1)
print(result)
# [[1 4]
# [2 5]
# [3 6]]
print(result.shape) # (3, 2)Split arrays into multiple sub-arrays:
arr = np.array([1, 2, 3, 4, 5, 6, 7, 8])
# Split into equal parts
parts = np.split(arr, 4) # Split into 4 arrays
print(parts) # [array([1, 2]), array([3, 4]), array([5, 6]), array([7, 8])]
# Split at specific indices
parts = np.split(arr, [3, 5]) # Split at indices 3 and 5
print(parts) # [array([1, 2, 3]), array([4, 5]), array([6, 7, 8])]Split 2D arrays:
matrix = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]])
# Split horizontally
left, right = np.hsplit(matrix, 2)
print(left)
# [[ 1 2]
# [ 5 6]
# [ 9 10]]
# Split vertically
top, bottom = np.vsplit(matrix, [2]) # Split at row 2
print(top)
# [[1 2 3 4]
# [5 6 7 8]]Advanced Indexing: Fancy Indexing and Boolean Masks
Beyond basic indexing and slicing, NumPy provides powerful selection mechanisms for complex data access patterns.
Fancy indexing uses arrays of indices:
arr = np.array([10, 20, 30, 40, 50])
# Select multiple elements by index
indices = np.array([0, 2, 4])
result = arr[indices]
print(result) # [10 30 50]
# Order matters
indices = np.array([4, 2, 0])
result = arr[indices]
print(result) # [50 30 10]
# Can select same index multiple times
indices = np.array([0, 0, 2, 2, 2])
result = arr[indices]
print(result) # [10 10 30 30 30]Fancy indexing with 2D arrays:
matrix = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# Select specific rows
rows = np.array([0, 2])
result = matrix[rows]
print(result)
# [[1 2 3]
# [7 8 9]]
# Select specific elements
rows = np.array([0, 1, 2])
cols = np.array([0, 1, 2])
result = matrix[rows, cols] # Diagonal elements
print(result) # [1 5 9]
# Select corners
rows = np.array([0, 0, 2, 2])
cols = np.array([0, 2, 0, 2])
result = matrix[rows, cols]
print(result) # [1 3 7 9]Boolean indexing using masks:
arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
# Select even numbers
mask = arr % 2 == 0
print(mask)
# [False True False True False True False True False True]
result = arr[mask]
print(result) # [ 2 4 6 8 10]
# More concisely
result = arr[arr % 2 == 0]
print(result) # [ 2 4 6 8 10]Combine multiple conditions:
arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
# Select values between 3 and 7
result = arr[(arr >= 3) & (arr <= 7)]
print(result) # [3 4 5 6 7]
# Select values outside range
result = arr[(arr < 3) | (arr > 7)]
print(result) # [ 1 2 8 9 10]Modify selected elements:
arr = np.array([1, 2, 3, 4, 5])
# Set values greater than 3 to 0
arr[arr > 3] = 0
print(arr) # [1 2 3 0 0]
# Increment even values
arr = np.array([1, 2, 3, 4, 5])
arr[arr % 2 == 0] += 10
print(arr) # [ 1 12 3 14 5]The np.where function provides three-way conditional selection:
arr = np.array([1, 2, 3, 4, 5, 6])
# Replace values: if > 3, use 1, else use 0
result = np.where(arr > 3, 1, 0)
print(result) # [0 0 0 1 1 1]
# Keep original value or replace
result = np.where(arr > 3, arr, 0)
print(result) # [0 0 0 4 5 6]
# Use different transformations
result = np.where(arr > 3, arr * 2, arr / 2)
print(result) # [0.5 1. 1.5 8. 10. 12. ]Find indices of elements:
arr = np.array([10, 20, 30, 40, 30, 20, 10])
# Find indices where condition is True
indices = np.where(arr == 30)
print(indices) # (array([2, 4]),)
# Use returned indices
print(arr[indices]) # [30 30]Sorting and Searching
NumPy provides efficient sorting and searching operations.
Sort arrays:
arr = np.array([3, 1, 4, 1, 5, 9, 2, 6])
# Sort (returns sorted copy)
sorted_arr = np.sort(arr)
print(sorted_arr) # [1 1 2 3 4 5 6 9]
print(arr) # [3 1 4 1 5 9 2 6] - original unchanged
# Sort in place
arr.sort()
print(arr) # [1 1 2 3 4 5 6 9]Get indices that would sort the array:
arr = np.array([3, 1, 4, 1, 5, 9, 2, 6])
# Get sorting indices
indices = np.argsort(arr)
print(indices) # [1 3 6 0 2 4 7 5]
# Use indices to sort
sorted_arr = arr[indices]
print(sorted_arr) # [1 1 2 3 4 5 6 9]Sort multi-dimensional arrays:
matrix = np.array([[3, 1, 4],
[1, 5, 9],
[2, 6, 5]])
# Sort each row
sorted_rows = np.sort(matrix, axis=1)
print(sorted_rows)
# [[1 3 4]
# [1 5 9]
# [2 5 6]]
# Sort each column
sorted_cols = np.sort(matrix, axis=0)
print(sorted_cols)
# [[1 1 4]
# [2 5 5]
# [3 6 9]]Search sorted arrays:
arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
# Find insertion index to maintain sorted order
index = np.searchsorted(arr, 5.5)
print(index) # 5 - insert at position 5
# Insert multiple values
indices = np.searchsorted(arr, [2.5, 5.5, 8.5])
print(indices) # [2 5 8]Find unique elements:
arr = np.array([1, 2, 2, 3, 3, 3, 4, 4, 5])
# Get unique values
unique = np.unique(arr)
print(unique) # [1 2 3 4 5]
# Count occurrences
unique, counts = np.unique(arr, return_counts=True)
print(unique) # [1 2 3 4 5]
print(counts) # [1 2 3 2 1]Universal Functions (ufuncs)
Universal functions operate element-wise on arrays, providing vectorized versions of many mathematical operations.
Mathematical ufuncs:
arr = np.array([1, 4, 9, 16, 25])
# Square root
print(np.sqrt(arr)) # [1. 2. 3. 4. 5.]
# Exponential
print(np.exp(arr)) # [2.718e+00 5.459e+01 8.103e+03 ...]
# Logarithm
print(np.log(arr)) # [0. 1.386 2.197 2.772 3.218]
# Trigonometric
angles = np.array([0, np.pi/2, np.pi])
print(np.sin(angles)) # [ 0. 1. 0.]
print(np.cos(angles)) # [ 1. 0. -1.]Rounding functions:
arr = np.array([1.23, 4.56, 7.89])
print(np.round(arr)) # [1. 5. 8.]
print(np.floor(arr)) # [1. 4. 7.]
print(np.ceil(arr)) # [2. 5. 8.]
print(np.trunc(arr)) # [1. 4. 7.]Comparison ufuncs:
arr1 = np.array([1, 2, 3])
arr2 = np.array([2, 2, 2])
print(np.equal(arr1, arr2)) # [False True False]
print(np.greater(arr1, arr2)) # [False False True]
print(np.less_equal(arr1, arr2)) # [ True True False]Binary ufuncs work on two arrays:
arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
print(np.add(arr1, arr2)) # [5 7 9] - same as arr1 + arr2
print(np.multiply(arr1, arr2)) # [ 4 10 18]
print(np.maximum(arr1, arr2)) # [4 5 6] - element-wise max
print(np.minimum(arr1, arr2)) # [1 2 3] - element-wise minLinear Algebra Operations
NumPy’s linear algebra module provides matrix operations essential for many data science algorithms.
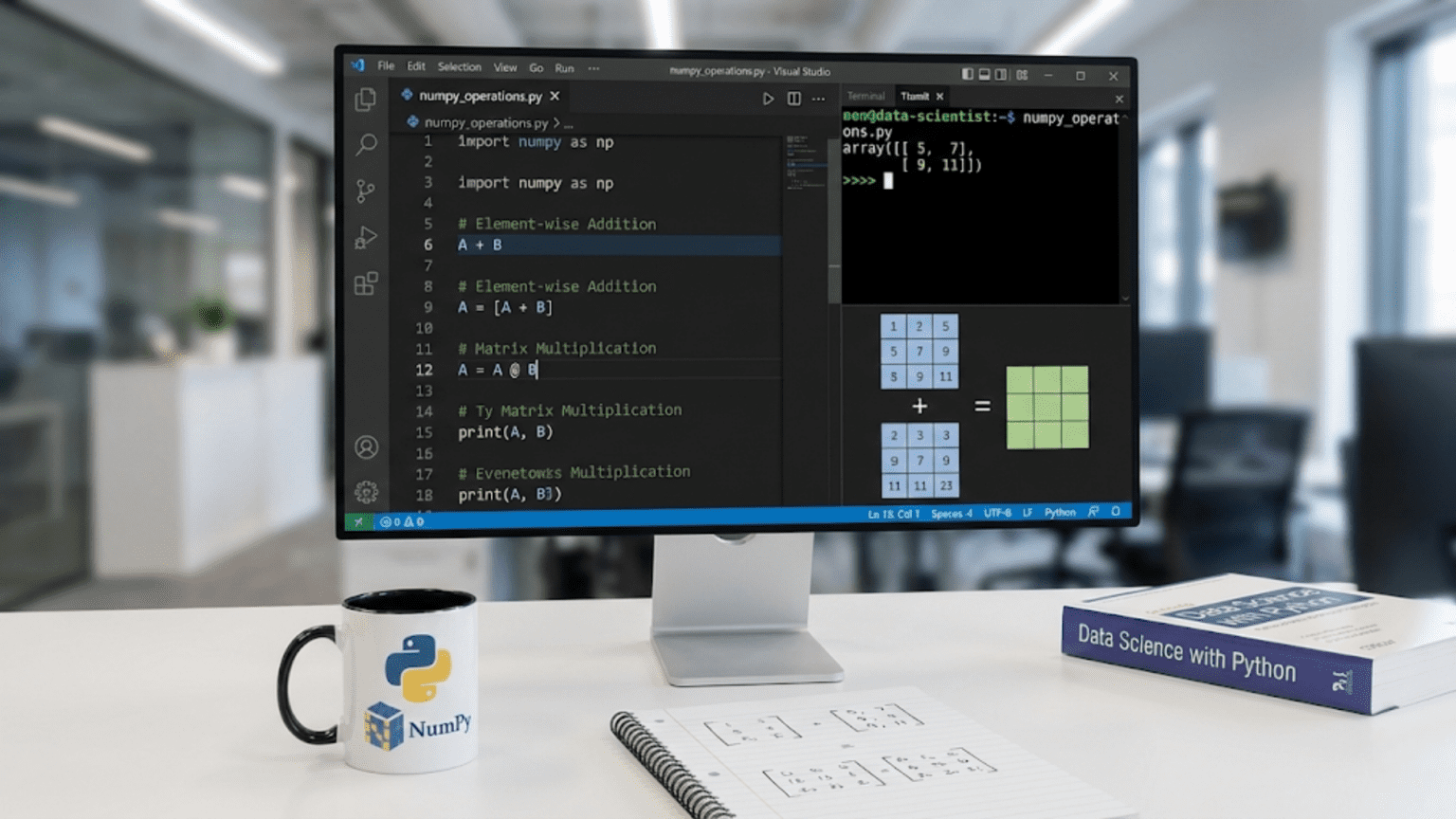
Matrix multiplication:
A = np.array([[1, 2],
[3, 4]])
B = np.array([[5, 6],
[7, 8]])
# Matrix multiplication
C = np.dot(A, B)
# Or
C = A @ B # Python 3.5+ operator
print(C)
# [[19 22]
# [43 50]]Transpose:
A = np.array([[1, 2, 3],
[4, 5, 6]])
print(A.T)
# [[1 4]
# [2 5]
# [3 6]]Matrix inverse:
A = np.array([[1, 2],
[3, 4]])
A_inv = np.linalg.inv(A)
print(A_inv)
# [[-2. 1. ]
# [ 1.5 -0.5]]
# Verify: A @ A_inv should be identity
print(A @ A_inv)
# [[1. 0.]
# [0. 1.]]Solve linear systems (Ax = b):
# Solve: 2x + 3y = 8, 4x + 5y = 14
A = np.array([[2, 3],
[4, 5]])
b = np.array([8, 14])
x = np.linalg.solve(A, b)
print(x) # [1. 2.]
# Verify
print(A @ x) # [ 8. 14.] - matches bEigenvalues and eigenvectors:
A = np.array([[1, 2],
[2, 1]])
eigenvalues, eigenvectors = np.linalg.eig(A)
print(eigenvalues) # [ 3. -1.]
print(eigenvectors)
# [[ 0.707 0.707]
# [ 0.707 -0.707]]Determinant:
A = np.array([[1, 2],
[3, 4]])
det = np.linalg.det(A)
print(det) # -2.0Practical Data Science Operations
Combine these operations for common data science tasks:
# Generate sample data
np.random.seed(42)
data = np.random.randn(100, 5) # 100 samples, 5 features
# Standardize (mean 0, std 1)
mean = data.mean(axis=0)
std = data.std(axis=0)
standardized = (data - mean) / std
# Verify
print(standardized.mean(axis=0)) # ~[0. 0. 0. 0. 0.]
print(standardized.std(axis=0)) # ~[1. 1. 1. 1. 1.]
# Find outliers (> 3 std from mean)
outliers = np.abs(standardized) > 3
print(f"Outliers: {outliers.sum()} out of {data.size}")
# Clip extreme values
clipped = np.clip(standardized, -3, 3)
# Calculate correlation matrix
correlation = np.corrcoef(data.T)
print(correlation.shape) # (5, 5)Performance Tips and Best Practices
Write efficient NumPy code by following these guidelines:
Vectorize operations instead of using loops:
# Slow - Python loop
result = []
for x in arr:
result.append(x ** 2)
# Fast - vectorized
result = arr ** 2Preallocate arrays when building incrementally:
# Slow - growing arrays
result = np.array([])
for i in range(1000):
result = np.append(result, i)
# Fast - preallocate
result = np.zeros(1000)
for i in range(1000):
result[i] = i
# Best - avoid loop entirely
result = np.arange(1000)Use views instead of copies when possible:
# Creates view (fast, shares memory)
view = arr[::2]
# Creates copy (slower, separate memory)
copy = arr[::2].copy()Use appropriate data types:
# Wastes memory - float64 is default
arr = np.array([1, 2, 3, 4, 5])
# More efficient for integers
arr = np.array([1, 2, 3, 4, 5], dtype=np.int32)
# Even more efficient if values fit
arr = np.array([1, 2, 3, 4, 5], dtype=np.int8)Conclusion
The NumPy operations covered in this guide, broadcasting, array combination, advanced indexing, sorting, universal functions, and linear algebra, represent essential tools for data science work. Mastering these operations enables you to manipulate data efficiently, write concise code that expresses intent clearly, and leverage NumPy’s full power for numerical computing. These patterns appear constantly in real data science projects, from data preprocessing through model training to results analysis.
The transition from thinking in loops to thinking in vectorized operations requires practice but pays enormous dividends in code clarity and performance. As you encounter data manipulation challenges, ask yourself how to express the operation using NumPy’s built-in capabilities rather than reaching for loops immediately. With experience, these patterns become second nature, and you will write NumPy code fluently.
These NumPy operations also prepare you for pandas, which builds directly on NumPy arrays and uses many similar patterns. Broadcasting, boolean indexing, vectorized operations, and the general principle of operating on entire data structures simultaneously transfer directly to pandas DataFrames. Master NumPy thoroughly, and you gain intuition that serves you throughout the scientific Python ecosystem. Practice these operations on real datasets, experiment with different approaches, and build the muscle memory that makes NumPy feel natural rather than foreign.