Clustering is one of the most fundamental techniques in unsupervised machine learning. Unlike supervised learning, where labeled data guides the learning process, clustering aims to group data points into clusters based on their inherent similarities. Among the various clustering algorithms available, K-Means is one of the most popular and widely used due to its simplicity and efficiency. This article serves as an introduction to K-Means, exploring its underlying concepts, mathematical framework, and practical applications.

What Is Clustering?

Clustering is a data analysis technique used to organize data points into meaningful groups, or clusters, such that objects within the same cluster are more similar to each other than to those in other clusters. It is widely used in domains like customer segmentation, image compression, and anomaly detection.

For example, a business might use clustering to segment its customers into groups based on purchasing behavior, allowing for targeted marketing strategies. Similarly, in healthcare, clustering can group patients based on symptoms to identify potential disease patterns.

Introduction to K-Means Clustering

K-Means is a centroid-based clustering algorithm that partitions a dataset into kkk clusters, where kkk is a user-defined parameter. Each cluster is represented by its centroid, which is the mean of all data points belonging to the cluster.

The objective of K-Means is to minimize the intra-cluster variance, ensuring that data points within a cluster are as close to their centroid as possible. Mathematically, the algorithm minimizes the following cost function:

Where:

• J is the total within-cluster variance.
• k is the number of clusters.
• C_i is the set of data points in the i-th cluster.
• μ_i​ is the centroid of the i-th cluster.
• ∥ x−μ_i ∥ ² is the squared distance between a data point x and its cluster centroid.

The K-Means Algorithm: Step-by-Step

The K-Means algorithm follows an iterative approach to partition the data into clusters. Below are the main steps involved:

Step 1: Initialization

The algorithm begins by selecting k initial centroids, which can be:

1. Randomly chosen data points.
2. Specified by the user.
3. Determined using advanced methods like the K-Means++ initialization to improve convergence.

Step 2: Assign Data Points to Clusters

Each data point is assigned to the nearest centroid based on a distance metric, typically Euclidean distance.

Step 3: Update Centroids

The centroid of each cluster is recalculated as the mean of all data points assigned to that cluster.

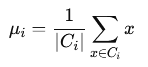
Where:

• ∣C_i∣ is the number of data points in cluster C_i.

Step 4: Repeat Until Convergence

Steps 2 and 3 are repeated until the centroids no longer change significantly, or a maximum number of iterations is reached.

Key Features of K-Means

1. Partitioning Technique: K-Means divides the dataset into k non-overlapping clusters.
2. Centroid-Based: Each cluster is represented by the mean of its data points.
3. Iterative Approach: The algorithm refines cluster assignments and centroids iteratively to achieve the optimal solution.

Applications of K-Means Clustering

K-Means has a wide range of real-world applications across industries, including:

1. Customer Segmentation

Businesses use K-Means to segment customers into groups based on purchasing patterns, demographics, or behavioral data. This helps in designing personalized marketing strategies.

2. Image Compression

In image processing, K-Means is used to reduce the number of colors in an image. By grouping similar colors into clusters, the algorithm compresses the image while preserving its visual quality.

3. Anomaly Detection

In cybersecurity, K-Means helps identify unusual patterns in network traffic, which could indicate potential security threats.

4. Document Clustering

In text analytics, K-Means groups similar documents based on word usage or topics, aiding in information retrieval and organization.

5. Genetic Data Analysis

In bioinformatics, K-Means clusters genetic data to identify patterns and similarities, contributing to advancements in personalized medicine.

Advantages of K-Means

1. Simplicity: The algorithm is easy to understand and implement.
2. Scalability: K-Means performs efficiently on large datasets.
3. Flexibility: It can handle a variety of data types and applications.
4. Speed: Convergence is often achieved in a relatively small number of iterations.

However, K-Means has its limitations, including sensitivity to the initial choice of centroids and difficulty in handling non-spherical clusters. These challenges will be discussed in detail in the subsequent sections.

Strengths of K-Means Clustering

K-Means is one of the most widely used clustering algorithms due to its numerous advantages:

1. Simplicity and Interpretability

K-Means is easy to understand and implement. Its output—clusters represented by centroids—is intuitive and straightforward to interpret.

2. Scalability

The algorithm is computationally efficient, making it suitable for large datasets. With a complexity of O(n⋅k⋅i), where n is the number of data points, k is the number of clusters, and i is the number of iterations, K-Means can handle datasets with millions of points effectively.

3. Flexibility

K-Means can be applied to a variety of domains and data types, as long as a meaningful distance metric can be defined.

4. Convergence

K-Means typically converges quickly to a solution, especially when the K-Means++ initialization is used.

5. Adaptability

By varying the value of k, K-Means can be tuned to provide different levels of granularity for clustering.

Limitations of K-Means Clustering

Despite its strengths, K-Means has several limitations that need to be addressed for effective usage:

1. Dependence on k

The user must specify the number of clusters (k) beforehand. Selecting the right k can be challenging and often requires domain knowledge or experimentation.

2. Sensitivity to Initialization

The choice of initial centroids significantly affects the final clusters. Poor initialization can lead to suboptimal solutions or slow convergence. Techniques like K-Means++ initialization mitigate this issue by carefully selecting initial centroids.

3. Assumes Spherical Clusters

K-Means works best when clusters are spherical and evenly distributed. For non-spherical clusters, the algorithm may incorrectly assign data points, resulting in poor clustering performance.

4. Sensitive to Outliers

Outliers can distort cluster centroids and affect the quality of clustering. Preprocessing steps like outlier detection and removal are essential to improve K-Means results.

5. Requires Numerical Data

K-Means relies on distance calculations, which means categorical variables must be transformed into numerical representations (e.g., using one-hot encoding) before applying the algorithm.

How to Determine the Optimal Number of Clusters (k)

One of the most critical decisions in K-Means clustering is determining the value of k. Several methods can help identify the optimal number of clusters:

1. Elbow Method

The Elbow Method involves plotting the Within-Cluster Sum of Squares (WCSS) against the number of clusters k. WCSS measures the total variance within each cluster. The “elbow point” in the graph, where the rate of decrease in WCSS slows down, suggests the optimal k.

2. Silhouette Score

The Silhouette Score evaluates the quality of clustering by measuring how similar a data point is to its own cluster compared to other clusters. The score ranges from -1 to 1, with higher values indicating better clustering. The optimal k maximizes the average Silhouette Score.

3. Gap Statistic

The Gap Statistic compares the clustering performance on the observed data to that on a reference dataset with no inherent structure. A significant gap indicates the optimal k.

Techniques to Optimize K-Means Clustering

1. K-Means++ Initialization

K-Means++ improves the initial selection of centroids, leading to faster convergence and better clustering. Instead of choosing centroids randomly, it spreads them out, ensuring that the initial centroids are far apart.

2. Preprocessing the Data

Preprocessing ensures the data is in an appropriate format for clustering:

• Standardization or Normalization: Rescales features to a uniform range, preventing features with larger scales from dominating the distance metric.
• Dimensionality Reduction: Techniques like PCA (Principal Component Analysis) reduce noise and improve clustering performance by eliminating irrelevant dimensions.

3. Handling Outliers

Outliers can be detected and removed using statistical methods or clustering-specific techniques. For instance:

• Z-score analysis identifies data points significantly far from the mean.
• Isolation Forests or DBSCAN can identify outliers as a preprocessing step.

4. Hybrid Approaches

Combining K-Means with other algorithms can enhance its performance:

• Hierarchical Clustering + K-Means: Use hierarchical clustering to determine the number of clusters and K-Means for final clustering.
• Density-Based Clustering + K-Means: Apply DBSCAN to remove outliers before running K-Means.

5. Repeated Runs

Run K-Means multiple times with different initializations and select the best clustering result based on the cost function or evaluation metrics.

Practical Example of K-Means in Python

Here’s a Python implementation of K-Means with the Elbow Method for determining k:

from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

# Generate synthetic data
X, _ = make_blobs(n_samples=500, centers=4, cluster_std=1.0, random_state=42)

# Elbow Method to determine optimal k
wcss = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, init='k-means++', random_state=42)
    kmeans.fit(X)
    wcss.append(kmeans.inertia_)

# Plot the Elbow Method
plt.plot(range(1, 11), wcss, marker='o')
plt.title('Elbow Method')
plt.xlabel('Number of Clusters')
plt.ylabel('WCSS')
plt.show()

# Fit K-Means with optimal k (e.g., 4)
optimal_k = 4
kmeans = KMeans(n_clusters=optimal_k, init='k-means++', random_state=42)
kmeans.fit(X)
labels = kmeans.labels_

This example demonstrates how to determine the optimal number of clusters and apply K-Means clustering effectively.

Advanced Variations of K-Means

Although K-Means is a robust and widely used algorithm, researchers have developed several variations to address its limitations and improve its performance. Some of the most notable ones include:

1. K-Medoids

K-Medoids, also known as Partitioning Around Medoids (PAM), is a variation of K-Means where centroids are replaced by medoids. A medoid is the most centrally located data point within a cluster. By using medoids instead of centroids, K-Medoids becomes less sensitive to outliers, making it suitable for datasets with noise or irregular distributions.

2. Mini-Batch K-Means

Mini-Batch K-Means is an efficient variant designed for large-scale datasets. Instead of processing the entire dataset at once, it uses small, random subsets (mini-batches) to update centroids iteratively. This significantly reduces computational cost and memory usage, making it ideal for streaming data or real-time clustering.

3. Fuzzy C-Means

Unlike traditional K-Means, which assigns each data point to a single cluster, Fuzzy C-Means allows data points to belong to multiple clusters with varying degrees of membership. This is particularly useful in applications where boundaries between clusters are not well-defined.

4. Weighted K-Means

Weighted K-Means assigns different weights to data points based on their importance or relevance. This is commonly used in cases where certain data points represent larger populations or carry more significance in the clustering process.

5. Kernel K-Means

Kernel K-Means extends the algorithm to non-linear cluster boundaries by applying kernel functions. This allows K-Means to handle complex, non-spherical clusters effectively. It is particularly useful in datasets where relationships between features are non-linear.

6. Bisecting K-Means

Bisecting K-Means is a hybrid approach combining hierarchical and partitioning methods. It begins with all data points in a single cluster and recursively splits them into two clusters using K-Means, creating a hierarchical structure. This method often produces better results than standard K-Means.

Challenges in Applying K-Means

Despite its widespread use, K-Means faces several practical challenges that require careful consideration:

1. Difficulty Handling Non-Spherical Clusters

K-Means assumes that clusters are spherical and evenly distributed. For datasets with elongated, irregular, or overlapping clusters, it may fail to produce meaningful groupings.

2. High Dimensionality

In high-dimensional spaces, the concept of distance becomes less meaningful due to the “curse of dimensionality.” Dimensionality reduction techniques like PCA or t-SNE are often necessary to preprocess the data before applying K-Means.

3. Sensitivity to Data Scaling

K-Means relies on distance metrics like Euclidean distance, making it sensitive to the scale of features. Features with larger scales can dominate the clustering process, leading to biased results. Feature scaling (e.g., normalization or standardization) is critical.

4. Predefined Number of Clusters

The need to specify k beforehand can be challenging, especially for datasets where the true number of clusters is unknown. Techniques like the Elbow Method and Silhouette Score are helpful but may not always provide a clear answer.

Best Practices for Applying K-Means

To overcome these challenges and maximize the effectiveness of K-Means, consider the following best practices:

1. Preprocess the Data

• Remove Outliers: Use statistical methods or clustering-based outlier detection to eliminate noise.
• Standardize Features: Ensure all features contribute equally by scaling them to a uniform range.
• Reduce Dimensionality: Use PCA or other techniques to eliminate irrelevant features and improve clustering performance.

2. Experiment with Different k Values

Run K-Means with various values of k and evaluate clustering performance using metrics like Silhouette Score, Gap Statistic, or Davies-Bouldin Index.

3. Use K-Means++ Initialization

Always use K-Means++ for centroid initialization to improve convergence and clustering quality.

4. Combine with Other Techniques

• Preprocess the data with density-based methods like DBSCAN to remove noise and outliers.
• Use hierarchical clustering to determine the approximate value of k.

Future Directions in Clustering

Clustering remains an active area of research, with significant advancements focused on improving existing algorithms and developing new methods. Future directions for K-Means and clustering techniques include:

1. Deep Clustering

Deep clustering combines neural networks with traditional clustering techniques. Neural networks extract complex features from raw data, which are then clustered using algorithms like K-Means. This approach has shown promise in applications like image and text clustering.

2. Automated Clustering

Automated clustering aims to eliminate the need for manual parameter tuning (e.g., selecting k) by integrating methods that adaptively determine the number of clusters based on the data.

3. Clustering for Streaming Data

With the rise of real-time applications, algorithms that can handle dynamic, streaming data are in high demand. Variants like Mini-Batch K-Means are already making progress in this area.

4. Explainable Clustering

As clustering results increasingly drive critical decisions, there is a growing need for explainable clustering models that provide insights into why certain data points are grouped together.

Conclusion

K-Means is a cornerstone algorithm in clustering, valued for its simplicity, scalability, and versatility. Its applications span a wide range of fields, from customer segmentation to image compression, making it an indispensable tool in data science. However, like any algorithm, K-Means has limitations that require careful handling, such as its sensitivity to initialization, dependence on k, and assumptions about cluster shapes.

By employing advanced techniques like K-Means++ initialization, dimensionality reduction, and hybrid approaches, practitioners can address these limitations and enhance clustering performance. Furthermore, understanding the nuances of the algorithm and its variations, such as K-Medoids and Mini-Batch K-Means, expands its applicability to more complex datasets and scenarios.

As clustering techniques evolve, K-Means remains a fundamental building block for unsupervised learning. Mastering its concepts and best practices is essential for anyone seeking to harness the power of data-driven insights.