Training, Validation, and Test Sets: Why We Split Data

Machine learning splits data into three sets to ensure models generalize to unseen data. The training set (typically 60-70%) teaches the model patterns, the validation set (15-20%) tunes hyperparameters and guides development decisions, and the test set (15-20%) provides final, unbiased performance evaluation. This separation prevents overfitting and provides honest estimates of how models will perform on new, real-world data.

Introduction: The Fundamental Challenge of Machine Learning

Imagine studying for an exam by memorizing answers to practice questions without truly understanding the underlying concepts. You might ace those exact practice questions, but when the actual exam presents similar but slightly different problems, you’d struggle. This is precisely the challenge machine learning models face—and why we split data into different sets.

The fundamental goal of machine learning isn’t to perform well on data we’ve already seen. Anyone can memorize answers. The goal is to generalize—to perform well on new, previously unseen data. A spam filter must identify spam it’s never encountered before. A medical diagnosis system must evaluate patients it hasn’t seen during training. A recommendation engine must suggest products for new users and new situations.

Data splitting is the mechanism that ensures our models actually generalize rather than merely memorize. By holding back portions of our data during training, we can evaluate how well models perform on data they haven’t seen, giving us honest estimates of real-world performance. This seemingly simple practice—dividing data into training, validation, and test sets—is absolutely fundamental to building reliable machine learning systems.

Yet data splitting is often misunderstood or improperly executed, leading to overly optimistic performance estimates and models that fail in production. This comprehensive guide explains why we split data, how to split it properly, common pitfalls to avoid, and best practices that ensure your models truly work when deployed.

Whether you’re building your first machine learning model or looking to deepen your understanding of evaluation methodology, mastering data splitting is essential. Let’s explore why this practice is so critical and how to do it right.

The Core Problem: Overfitting and Generalization

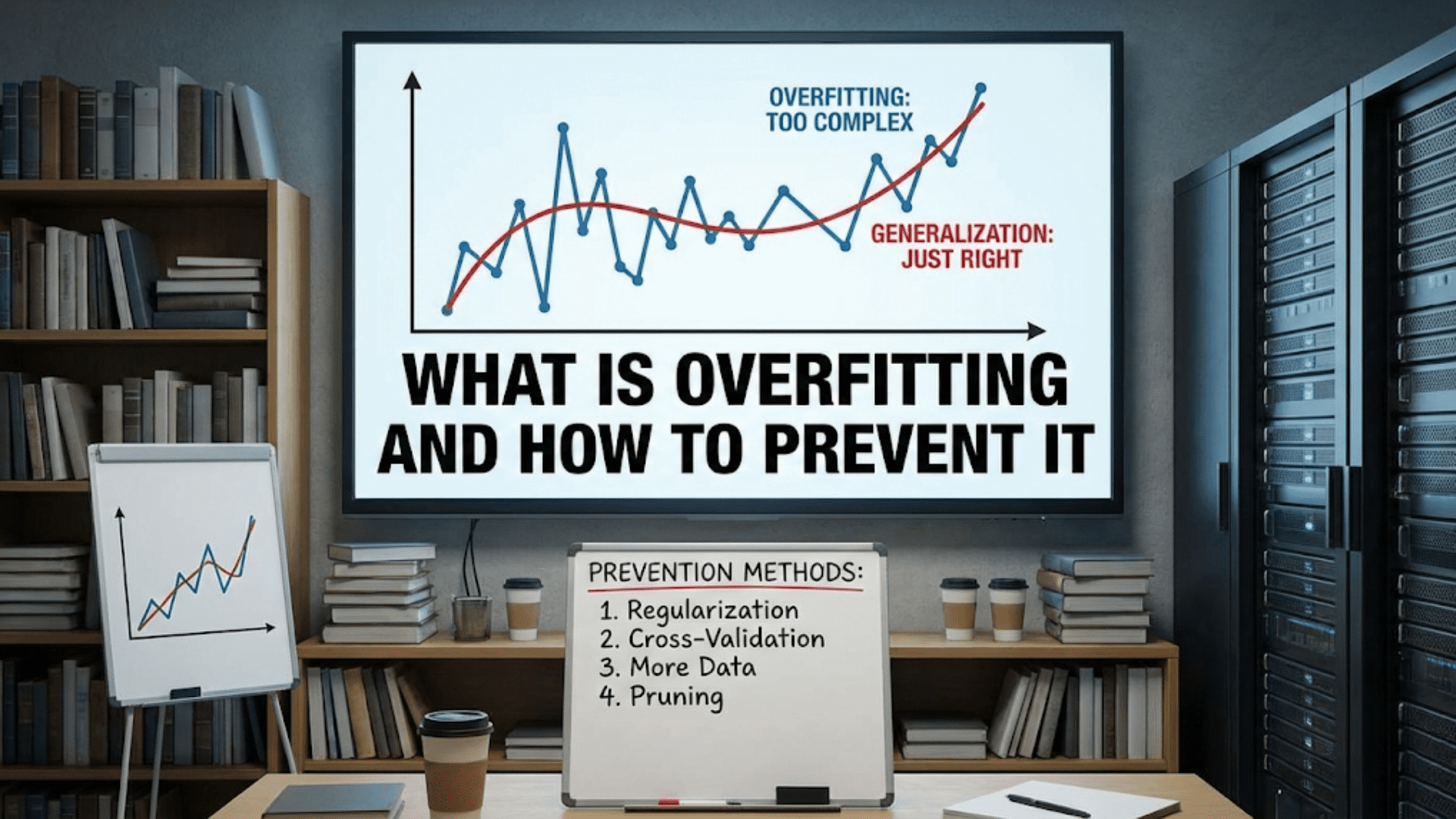
To understand why we split data, we must first understand the challenge that splitting addresses: overfitting.

What is Overfitting?

Overfitting occurs when a model learns patterns specific to the training data—including noise and random fluctuations—rather than learning the underlying true patterns that generalize to new data.

Example: Memorization vs. Understanding

Imagine teaching a child to identify animals using a specific set of 20 photos. If the child memorizes “the photo with the red barn has a horse” rather than learning what horses actually look like, they’ve overfit. They’ll correctly identify horses in those 20 photos but fail when shown new horse photos.

Similarly, a machine learning model might learn “data point 42 has label A” rather than learning the pattern of features that characterize label A. It performs perfectly on training data but poorly on new data.

The Generalization Gap

The difference between a model’s performance on training data and its performance on new data is called the generalization gap. Large gaps indicate overfitting.

Example Performance:

• Training accuracy: 99%
• New data accuracy: 65%
• Generalization gap: 34 percentage points

This model has clearly overfit—it memorized the training data but doesn’t truly understand the underlying patterns.

Why Models Overfit

Several factors contribute to overfitting:

Model Complexity: More complex models (more parameters) can fit data more precisely, including noise. A model with millions of parameters can memorize a dataset of thousands of examples.

Insufficient Data: With limited training examples, models may learn spurious patterns that happen to occur in the small sample but don’t reflect reality.

Training Too Long: Models may initially learn general patterns, then gradually overfit as training continues, learning training set quirks.

Noise in Data: Mislabeled examples, measurement errors, or random variations can be learned as if they were true patterns.

Feature-to-Sample Ratio: Many features relative to few samples makes overfitting likely (curse of dimensionality).

The Need for Evaluation on Unseen Data

If we only evaluate models on data they’ve seen during training, we can’t detect overfitting. The model might have 100% training accuracy through pure memorization while being useless for actual predictions.

We need to evaluate on data the model hasn’t seen—data held back specifically for evaluation. This is where data splitting comes in.

The Three Sets: Training, Validation, and Test

Modern machine learning practice typically divides data into three distinct sets, each serving a specific purpose.

Training Set: Where Learning Happens

Purpose: Teach the model patterns in the data

Usage:

• Feed to the learning algorithm
• Algorithm adjusts model parameters to minimize errors on this data
• Model sees this data during the training process

Typical Size: 60-70% of total data

Example: If you have 10,000 data points, use 6,000-7,000 for training

The training set is where the actual learning occurs. The model iteratively adjusts its parameters to better predict the training set labels. All the pattern recognition, weight adjustment, and optimization happens using training data.

Key Principle: The model is allowed—even expected—to perform very well on training data. High training performance alone doesn’t indicate a good model.

Validation Set: For Model Development

Purpose: Guide model development decisions without biasing final evaluation

Usage:

• Evaluate different model configurations
• Tune hyperparameters (learning rate, regularization strength, model architecture)
• Decide when to stop training
• Compare different models or features
• Make any decision during model development

Typical Size: 15-20% of total data

Example: With 10,000 data points, use 1,500-2,000 for validation

The validation set addresses a subtle but important problem: if we make many development decisions based on test set performance, we effectively “learn” from the test set, introducing bias. The validation set lets us iterate and experiment without compromising our final evaluation.

Development Workflow:

1. Train model on training set
2. Evaluate on validation set
3. Adjust hyperparameters, features, or architecture
4. Repeat until validation performance is satisfactory
5. Only then evaluate on test set

Test Set: For Final Evaluation

Purpose: Provide unbiased estimate of model performance on new data

Usage:

• Evaluate model only once, after all development is complete
• Report final performance metrics
• Compare with baseline or existing solutions
• Decide whether to deploy

Typical Size: 15-20% of total data

Example: With 10,000 data points, use 1,500-2,000 for testing

The test set is sacred—it should remain completely untouched until you’re ready for final evaluation. Looking at test performance during development, even just to check progress, introduces bias.

Key Principle: The test set should simulate completely new, unseen data as closely as possible. It provides the most honest estimate of how your model will perform in production.

Why Three Sets Instead of Just Two?

You might wonder: why not just training and test sets?

Two-Set Problem: If you use the test set to make development decisions (choosing hyperparameters, selecting features, comparing models), you’re indirectly optimizing for test set performance. Over many iterations, you’ll select configurations that happen to work well on the test set, potentially by chance. Your test set performance becomes an optimistically biased estimate.

Three-Set Solution: The validation set absorbs this bias. You can iterate freely using validation performance without compromising your test set. The test set remains a truly independent evaluation, untouched by the development process.

Analogy:

• Training set: Study materials you actively learn from
• Validation set: Practice exams you take repeatedly to assess readiness and adjust study approach
• Test set: The actual final exam, taken once to measure true understanding

Data Splitting Methods and Best Practices

How you split data matters tremendously. Improper splitting can invalidate your evaluation.

Random Splitting

The simplest approach: randomly assign each example to training, validation, or test.

Process:

1. Shuffle data randomly
2. Take first 70% for training
3. Take next 15% for validation
4. Take final 15% for test

When Appropriate:

• Data points are independent
• No temporal ordering
• Target distribution is consistent
• Sufficient data in all sets

Example Implementation:

from sklearn.model_selection import train_test_split

# First split: separate out test set
train_val, test = train_test_split(data, test_size=0.15, random_state=42)

# Second split: separate training and validation
train, validation = train_test_split(train_val, test_size=0.176, random_state=42)
# 0.176 of remaining 85% gives 15% of original

from sklearn.model_selection import train_test_split

# First split: separate out test set
train_val, test = train_test_split(data, test_size=0.15, random_state=42)

# Second split: separate training and validation
train, validation = train_test_split(train_val, test_size=0.176, random_state=42)
# 0.176 of remaining 85% gives 15% of original

Advantages:

• Simple and straightforward
• Works well for many problems
• Easy to implement

Limitations:

• May create unrepresentative splits by chance
• Doesn’t respect temporal ordering
• May not maintain class balance

Stratified Splitting

Ensures each split maintains the same class distribution as the overall dataset.

Purpose: Prevent skewed splits where one set has very different proportions of classes

Example Problem:

• Overall data: 80% class A, 20% class B
• Random split might yield validation set with 90% class A, 10% class B
• Training on imbalanced data while validating on different distribution misleads

Stratified Solution:

• Each split has same 80/20 distribution
• Training, validation, and test all representative of overall data

Implementation:

# Stratified split maintains class proportions
train_val, test = train_test_split(
    data, test_size=0.15, stratify=labels, random_state=42
)

# Stratified split maintains class proportions
train_val, test = train_test_split(
    data, test_size=0.15, stratify=labels, random_state=42
)

When to Use:

• Classification problems with imbalanced classes
• Want to ensure all sets are representative
• Small datasets where random chance might create skewed splits

Time-Based Splitting

For temporal data, respect time ordering by using past to predict future.

Principle: Training data comes before validation data, which comes before test data

Example Timeline:

• Training: January 2022 – December 2023 (24 months)
• Validation: January 2024 – March 2024 (3 months)
• Test: April 2024 – June 2024 (3 months)

Why Critical for Temporal Data:

Problem with Random Splitting: If you randomly split time series data, you might train on July data and test on June data—using the future to predict the past. This causes data leakage, inflating performance estimates.

Real-World Alignment: In production, you always predict future events based on past data. Time-based splitting simulates this.

Concept Drift Detection: Temporal splitting reveals if model performance degrades over time as patterns change.

When to Use:

• Stock price prediction
• Sales forecasting
• Customer churn prediction
• Any problem with temporal dependency
• Sequential data

Example:

# Sort by timestamp
data_sorted = data.sort_values('timestamp')

# Split by time
train_end = '2023-12-31'
val_end = '2024-03-31'

train = data_sorted[data_sorted['timestamp'] <= train_end]
validation = data_sorted[
    (data_sorted['timestamp'] > train_end) & 
    (data_sorted['timestamp'] <= val_end)
]
test = data_sorted[data_sorted['timestamp'] > val_end]

# Sort by timestamp
data_sorted = data.sort_values('timestamp')

# Split by time
train_end = '2023-12-31'
val_end = '2024-03-31'

train = data_sorted[data_sorted['timestamp'] <= train_end]
validation = data_sorted[
    (data_sorted['timestamp'] > train_end) & 
    (data_sorted['timestamp'] <= val_end)
]
test = data_sorted[data_sorted['timestamp'] > val_end]

Group-Based Splitting

Ensure related examples stay together in the same split.

Purpose: Prevent data leakage when multiple examples relate to the same entity

Example Problem: Medical diagnosis with multiple scans per patient

• Patient A has 10 scans (8 diseased, 2 healthy)
• Random splitting might put 7 scans in training, 3 in test
• Model learns Patient A’s specific characteristics
• Artificially high performance because it recognizes the same patient

Solution: Keep all scans from the same patient in the same split

When to Use:

• Multiple measurements per individual (patients, customers, sensors)
• Related documents (multiple articles from same source)
• Temporal sequences for same entity
• Any hierarchical or grouped data structure

Implementation:

from sklearn.model_selection import GroupShuffleSplit

# Ensure all data from same patient stays together
splitter = GroupShuffleSplit(n_splits=1, test_size=0.15, random_state=42)
train_idx, test_idx = next(splitter.split(data, groups=patient_ids))

from sklearn.model_selection import GroupShuffleSplit

# Ensure all data from same patient stays together
splitter = GroupShuffleSplit(n_splits=1, test_size=0.15, random_state=42)
train_idx, test_idx = next(splitter.split(data, groups=patient_ids))

Geographic or Demographic Splitting

Test model’s ability to generalize across locations or populations.

Purpose: Evaluate if model works for different regions or demographic groups

Example:

• Train on data from 10 cities
• Validate on data from 5 different cities
• Test on data from 5 completely different cities
• Reveals if model generalizes geographically or just learns city-specific patterns

When to Use:

• Model will be deployed to new locations
• Testing fairness across demographic groups
• Want to ensure no region-specific overfitting

Common Data Splitting Pitfalls

Several mistakes commonly compromise evaluation validity:

Pitfall 1: Data Leakage Through Improper Splitting

Problem: Information from validation/test sets leaks into training

Example 1 – Temporal Leakage:

Wrong: Random split of time series → training contains future data
Right: Temporal split → training only contains past data

Wrong: Random split of time series → training contains future data
Right: Temporal split → training only contains past data

Example 2 – Group Leakage:

Wrong: Split patient scans randomly → same patient in train and test
Right: Group by patient → each patient's scans all in same set

Wrong: Split patient scans randomly → same patient in train and test
Right: Group by patient → each patient's scans all in same set

Example 3 – Feature Engineering Leakage:

Wrong: Calculate feature statistics on entire dataset, then split
Right: Split first, calculate statistics only on training set

Wrong: Calculate feature statistics on entire dataset, then split
Right: Split first, calculate statistics only on training set

Consequences: Inflated performance estimates, models fail in production

Solution:

• Split data before any processing
• Respect temporal ordering
• Keep related examples together
• Calculate all statistics only on training data

Pitfall 2: Using Test Set During Development

Problem: Peeking at test performance while developing model

Example:

• Check test accuracy after each experiment
• Try 20 different models, picking the one with best test performance
• Report that best test performance as model performance

Why Problematic: You’ve effectively optimized for test set performance through selection, introducing bias

Consequences: Overly optimistic performance estimates

Solution:

• Use validation set for all development decisions
• Look at test set only once, after development is complete
• If test performance is disappointing, resist urge to iterate more—this would bias test set

Pitfall 3: Improper Stratification

Problem: Splits have different class distributions

Example:

• Overall data: 10% positive class
• Training: 8% positive class
• Validation: 15% positive class
• Test: 12% positive class

Consequences:

• Model trains on different distribution than it’s evaluated on
• Misleading performance comparisons
• May learn wrong decision thresholds

Solution: Use stratified splitting for classification problems

Pitfall 4: Too Small Validation/Test Sets

Problem: Insufficient data in validation or test sets

Example:

• 100,000 training examples
• 100 validation examples
• 50 test examples

Consequences:

• High variance in validation/test performance estimates
• Small differences might be random chance
• Can’t reliably compare models

Solution:

• Ensure validation/test sets large enough for stable estimates
• Minimum: ~1,000 examples for test set when possible
• More needed for rare classes or high-stakes decisions
• Use cross-validation if total data is limited

Pitfall 5: Not Splitting At All

Problem: Evaluating on same data used for training

Consequences:

• Can’t detect overfitting
• No idea how model performs on new data
• Nearly useless for assessing model quality

Solution: Always split data, no matter how limited your dataset

Pitfall 6: Splitting After Data Augmentation

Problem: Augmented versions of same original data in different splits

Example:

• Original image A
• Create augmented versions: A_rotated, A_flipped, A_cropped
• Random splitting puts some in training, some in validation
• Validation includes slight variations of training data

Consequences: Inflated validation performance

Solution:

• Split first based on original data
• Augment only training data after splitting
• Keep original data in only one split

Pitfall 7: Inconsistent Preprocessing

Problem: Different preprocessing for different sets

Example:

• Normalize training data using its mean and std
• Normalize validation data using its own mean and std
• Normalize test data using its own mean and std

Consequences: Data distributions don’t match, unfair evaluation

Solution:

• Calculate preprocessing parameters (mean, std, min, max) only on training data
• Apply same parameters to validation and test data
• This simulates production: you’ll use training statistics for new data

Optimal Split Ratios: How Much Data for Each Set?

The ideal split depends on your total data size and problem characteristics.

Standard Splits for Moderate Datasets

Common Ratio: 70-15-15 or 60-20-20

10,000 Examples:

• Training: 7,000 (70%)
• Validation: 1,500 (15%)
• Test: 1,500 (15%)

This provides enough training data for learning while maintaining sufficient validation and test data for reliable evaluation.

Large Datasets

With 1,000,000+ examples, percentages can shift:

• Training: 98% (980,000)
• Validation: 1% (10,000)
• Test: 1% (10,000)

Rationale:

• 10,000 examples provides stable performance estimates
• Maximizing training data improves model learning
• Smaller percentages still yield large absolute numbers

Small Datasets

With 1,000 examples, standard splits become problematic:

• Training: 700 might be insufficient for learning
• Validation: 150 too small for reliable tuning
• Test: 150 too small for reliable final evaluation

Solutions:

• Use cross-validation instead of fixed validation set
• Consider 80-20 split (training-test) with cross-validation on training portion
• Collect more data if possible
• Be very careful about overfitting

Factors Influencing Split Ratios

Model Complexity:

• Simple models: Can learn from less data, allocate more to validation/test
• Complex models: Need more training data

Problem Difficulty:

• Easy patterns: Less training data needed
• Subtle patterns: More training data needed

Class Balance:

• Balanced classes: Standard splits work
• Rare classes: Need larger validation/test to ensure sufficient rare examples

Data Collection Cost:

• Expensive labeling: Maximize training data use
• Cheap data: Can afford larger validation/test sets

Practical Example: Customer Churn Prediction

Let’s walk through a complete example to see data splitting in practice.

Problem Setup

Objective: Predict which customers will cancel subscriptions in next 30 days

Available Data: 50,000 customers with:

• Customer features: Demographics, usage patterns, billing history
• Label: Did they churn? (Binary: Yes/No)
• Timeframe: January 2022 – June 2024
• Class distribution: 15% churned, 85% retained

Splitting Strategy Decision

Considerations:

1. Temporal nature: Customer behavior evolves over time
2. Class imbalance: Need stratification to maintain 15/85 split
3. Business use case: Will predict future churn from current data

Decision: Use temporal split with stratification

Implementation

Step 1: Sort by Time

Organize customers by when we observed them

Organize customers by when we observed them

Step 2: Define Split Points

Training: Jan 2022 - Dec 2023 (24 months)
Validation: Jan 2024 - Mar 2024 (3 months)  
Test: Apr 2024 - Jun 2024 (3 months)

Training: Jan 2022 - Dec 2023 (24 months)
Validation: Jan 2024 - Mar 2024 (3 months)  
Test: Apr 2024 - Jun 2024 (3 months)

Step 3: Extract Customers

Training: 35,000 customers
Validation: 7,500 customers
Test: 7,500 customers

Training: 35,000 customers
Validation: 7,500 customers
Test: 7,500 customers

Step 4: Verify Stratification

Training: 15.2% churn rate (close to 15%)
Validation: 14.8% churn rate
Test: 15.1% churn rate
Good - all sets representative

Training: 15.2% churn rate (close to 15%)
Validation: 14.8% churn rate
Test: 15.1% churn rate
Good - all sets representative

Feature Engineering Considerations

Calculate Only on Training Data:

Correct:

# Calculate statistics on training data
mean_usage = train_data['usage'].mean()
std_usage = train_data['usage'].std()

# Apply to all sets
train_data['usage_normalized'] = (train_data['usage'] - mean_usage) / std_usage
val_data['usage_normalized'] = (val_data['usage'] - mean_usage) / std_usage
test_data['usage_normalized'] = (test_data['usage'] - mean_usage) / std_usage

# Calculate statistics on training data
mean_usage = train_data['usage'].mean()
std_usage = train_data['usage'].std()

# Apply to all sets
train_data['usage_normalized'] = (train_data['usage'] - mean_usage) / std_usage
val_data['usage_normalized'] = (val_data['usage'] - mean_usage) / std_usage
test_data['usage_normalized'] = (test_data['usage'] - mean_usage) / std_usage

Wrong:

# Don't do this! Uses validation/test data in normalization
mean_usage = all_data['usage'].mean()  # Includes validation and test

# Don't do this! Uses validation/test data in normalization
mean_usage = all_data['usage'].mean()  # Includes validation and test

Aggregation Features:

Create features like “average usage” or “churn rate by segment” using only training data:

# Segment churn rates from training data only
segment_churn_rates = train_data.groupby('segment')['churned'].mean()

# Apply to all sets
train_data['segment_churn_rate'] = train_data['segment'].map(segment_churn_rates)
val_data['segment_churn_rate'] = val_data['segment'].map(segment_churn_rates)
test_data['segment_churn_rate'] = test_data['segment'].map(segment_churn_rates)

# Segment churn rates from training data only
segment_churn_rates = train_data.groupby('segment')['churned'].mean()

# Apply to all sets
train_data['segment_churn_rate'] = train_data['segment'].map(segment_churn_rates)
val_data['segment_churn_rate'] = val_data['segment'].map(segment_churn_rates)
test_data['segment_churn_rate'] = test_data['segment'].map(segment_churn_rates)

Model Development Workflow

Phase 1: Initial Training

Train baseline logistic regression on training set
Evaluate on validation set
Validation Accuracy: 82%
Validation F1 Score: 0.45

Train baseline logistic regression on training set
Evaluate on validation set
Validation Accuracy: 82%
Validation F1 Score: 0.45

Phase 2: Hyperparameter Tuning

Try different regularization strengths: 0.001, 0.01, 0.1, 1.0
Evaluate each on validation set
Best: regularization = 0.1
Validation F1 Score: 0.51

Try different regularization strengths: 0.001, 0.01, 0.1, 1.0
Evaluate each on validation set
Best: regularization = 0.1
Validation F1 Score: 0.51

Phase 3: Feature Engineering

Add engineered features:
- Days since last login
- Usage trend (increasing/decreasing)
- Support ticket count
Train with new features
Validation F1 Score: 0.58

Add engineered features:
- Days since last login
- Usage trend (increasing/decreasing)
- Support ticket count
Train with new features
Validation F1 Score: 0.58

Phase 4: Model Comparison

Try different algorithms:
- Logistic Regression: 0.58
- Random Forest: 0.62
- Gradient Boosting: 0.67
- Neural Network: 0.64
Select Gradient Boosting based on validation performance

Try different algorithms:
- Logistic Regression: 0.58
- Random Forest: 0.62
- Gradient Boosting: 0.67
- Neural Network: 0.64
Select Gradient Boosting based on validation performance

Phase 5: Final Optimization

Tune gradient boosting hyperparameters on validation set
Final validation F1 Score: 0.69

Tune gradient boosting hyperparameters on validation set
Final validation F1 Score: 0.69

Phase 6: Test Evaluation (ONLY ONCE)

Evaluate final model on test set
Test F1 Score: 0.66
Test Accuracy: 84%

Evaluate final model on test set
Test F1 Score: 0.66
Test Accuracy: 84%

Results Interpretation

Training Performance: 92% accuracy, F1: 0.85 Validation Performance: 86% accuracy, F1: 0.69 Test Performance: 84% accuracy, F1: 0.66

Analysis:

• Training vs. Validation gap: Model slightly overfit (92% vs 86%)
• Validation vs. Test: Small difference (0.69 vs 0.66), validation set provided good estimate
• Test performance: Honest estimate of production performance
• Decision: Deploy model, expect ~84% accuracy and F1 ~0.66 in production

Production Monitoring

After deployment, monitor actual performance:

Month 1: 83% accuracy - matches test estimate
Month 2: 82% accuracy - slight decline, within expected range
Month 3: 79% accuracy - concerning decline, investigate concept drift

Month 1: 83% accuracy - matches test estimate
Month 2: 82% accuracy - slight decline, within expected range
Month 3: 79% accuracy - concerning decline, investigate concept drift

Because we have unbiased test set estimates, we can detect when production performance deviates from expectations.

Advanced Splitting Techniques

Beyond basic splits, several advanced approaches address special situations.

K-Fold Cross-Validation

Instead of single validation set, use multiple different validation sets.

Process:

1. Divide data into K folds (typically 5 or 10)
2. For each fold:
   • Use that fold as validation
   • Use remaining K-1 folds as training
   • Train and evaluate model
3. Average performance across all K folds

Advantages:

• More robust performance estimate
• Uses all data for both training and validation
• Reduces variance in performance estimates

Disadvantages:

• K times more expensive (K training runs)
• More complex implementation

When to Use:

• Small datasets where fixed validation set is too small
• Want robust performance estimates
• Comparing multiple models

Note: Still keep separate test set for final evaluation. Cross-validation replaces fixed validation set, not test set.

Nested Cross-Validation

Cross-validation for both model selection and final evaluation.

Structure:

• Outer loop: K-fold cross-validation for final performance estimate
• Inner loop: Cross-validation for hyperparameter tuning

Purpose: Completely unbiased performance estimate even when tuning hyperparameters

When to Use:

• Small datasets where separate test set is impractical
• Need most rigorous performance estimate
• Publishing research requiring unbiased results

Trade-off: Very computationally expensive (K × K training runs)

Time Series Cross-Validation

Multiple train-validation splits respecting temporal order.

Expanding Window:

Split 1: Train [1-100], Validate [101-120]
Split 2: Train [1-120], Validate [121-140]
Split 3: Train [1-140], Validate [141-160]

Split 1: Train [1-100], Validate [101-120]
Split 2: Train [1-120], Validate [121-140]
Split 3: Train [1-140], Validate [141-160]

Sliding Window:

Split 1: Train [1-100], Validate [101-120]
Split 2: Train [21-120], Validate [121-140]
Split 3: Train [41-140], Validate [141-160]

Split 1: Train [1-100], Validate [101-120]
Split 2: Train [21-120], Validate [121-140]
Split 3: Train [41-140], Validate [141-160]

Purpose:

• Test model with different amounts of historical data
• Evaluate stability over time
• Detect concept drift

Stratified Group K-Fold

Combines stratification and group splitting with cross-validation.

Purpose:

• Maintain class balance (stratification)
• Keep groups together (group splitting)
• Get robust estimates (cross-validation)

Example: Medical data with multiple scans per patient and rare diseases

• Need: Balanced classes, patients not split, robust estimates
• Solution: Stratified group K-fold

Data Splitting for Special Cases

Certain scenarios require adapted splitting strategies.

Imbalanced Datasets

Challenge: Rare positive class (e.g., 1% fraud, 99% legitimate)

Standard Split Problem:

• Test set with 150 examples might have only 1-2 positive examples
• Can’t reliably measure performance

Solutions:

• Stratified splitting: Ensure test set has sufficient positive examples
• Larger test set: Maybe 25-30% to get enough rare examples
• Specialized metrics: Don’t rely on accuracy; use precision, recall, F1

Multi-Label Problems

Challenge: Examples can have multiple labels simultaneously

Solution:

• Stratified splitting becomes complex
• Consider iterative stratification algorithms
• Ensure all labels represented in all sets

Hierarchical Data

Challenge: Data has nested structure (students within schools, measurements within patients)

Solution:

• Group splitting at appropriate level
• Keep hierarchy intact in each split
• Consider hierarchical cross-validation

Small Datasets

Challenge: Only 500 examples total

Solutions:

• Use cross-validation instead of fixed splits
• Consider leave-one-out cross-validation (extreme: N folds for N examples)
• Be very conservative about model complexity
• Collect more data if possible

Evaluating Your Splits

After splitting, verify your splits are appropriate:

Class Distribution Check

# Verify similar distributions
print(f"Training churn rate: {train_labels.mean():.3f}")
print(f"Validation churn rate: {val_labels.mean():.3f}")
print(f"Test churn rate: {test_labels.mean():.3f}")

# Should be similar, e.g., all around 0.15

# Verify similar distributions
print(f"Training churn rate: {train_labels.mean():.3f}")
print(f"Validation churn rate: {val_labels.mean():.3f}")
print(f"Test churn rate: {test_labels.mean():.3f}")

# Should be similar, e.g., all around 0.15

Feature Distribution Check

# Compare feature distributions
train_features.describe()
val_features.describe()
test_features.describe()

# Visualize
for col in features:
    plot_distribution_comparison(train[col], val[col], test[col])

# Compare feature distributions
train_features.describe()
val_features.describe()
test_features.describe()

# Visualize
for col in features:
    plot_distribution_comparison(train[col], val[col], test[col])

Temporal Validity Check

# Verify no temporal leakage
assert train_dates.max() < val_dates.min()
assert val_dates.max() < test_dates.min()

# Verify no temporal leakage
assert train_dates.max() < val_dates.min()
assert val_dates.max() < test_dates.min()

Size Check

# Ensure sufficient examples
print(f"Training size: {len(train)}")
print(f"Validation size: {len(val)}")
print(f"Test size: {len(test)}")

# Validate minimums (depends on problem)
assert len(val) >= 1000  # Example minimum
assert len(test) >= 1000

# Ensure sufficient examples
print(f"Training size: {len(train)}")
print(f"Validation size: {len(val)}")
print(f"Test size: {len(test)}")

# Validate minimums (depends on problem)
assert len(val) >= 1000  # Example minimum
assert len(test) >= 1000

Independence Check

# Verify no overlap
assert len(set(train_ids) & set(val_ids)) == 0
assert len(set(train_ids) & set(test_ids)) == 0
assert len(set(val_ids) & set(test_ids)) == 0

# Verify no overlap
assert len(set(train_ids) & set(val_ids)) == 0
assert len(set(train_ids) & set(test_ids)) == 0
assert len(set(val_ids) & set(test_ids)) == 0

Best Practices Summary

Follow these guidelines for effective data splitting:

Before Splitting

1. Understand your data structure: Temporal? Grouped? Hierarchical?
2. Identify dependencies: Related examples that must stay together?
3. Check class distribution: Imbalanced? Need stratification?
4. Determine use case: How will model be used in production?

During Splitting

1. Split first: Before any preprocessing or feature engineering
2. Maintain temporal order: For time-series or sequential data
3. Keep groups together: For grouped or hierarchical data
4. Stratify when needed: For imbalanced classification
5. Document decisions: Record splitting strategy and rationale

After Splitting

1. Validate splits: Check distributions, sizes, independence
2. Use training data only: For calculating preprocessing parameters
3. Reserve test set: Don’t touch until final evaluation
4. Iterate on validation: Use freely for development
5. Evaluate once on test: Report final, unbiased performance

Production Considerations

1. Monitor performance: Compare production results to test estimates
2. Watch for drift: Detect when patterns change over time
3. Retrain periodically: Use new data to keep model current
4. Maintain split strategy: Use same splitting approach for retraining

Comparison: Split Strategies

Conclusion: The Foundation of Reliable Evaluation

Data splitting is not just a technical formality—it’s the foundation of reliable machine learning evaluation. Without proper splits, you have no way to know whether your model actually works or has simply memorized training data. Production deployments based on improperly validated models fail predictably and expensively.

The three-set paradigm—training, validation, and test—provides a robust framework for development and evaluation:

Training data enables learning, giving the model examples to learn patterns from.

Validation data guides development, letting you iterate and experiment without biasing your final evaluation.

Test data provides honest assessment, giving you an unbiased estimate of real-world performance.

Proper splitting requires careful consideration of your data structure, problem characteristics, and deployment context. Temporal data needs time-based splits. Grouped data requires keeping groups together. Imbalanced classes benefit from stratification. Small datasets call for cross-validation.

Common pitfalls—data leakage, improper stratification, peeking at test data, inconsistent preprocessing—can invalidate your evaluation, leading to overly optimistic estimates and failed deployments. Avoiding these mistakes requires discipline and understanding of why each practice matters.

The split ratios themselves matter less than the principles: enough training data for learning, sufficient validation data for stable development decisions, adequate test data for reliable final evaluation. Adjust percentages based on your total data size, but maintain the separation of purposes.

Remember that data splitting simulates the fundamental machine learning challenge: performing well on new, unseen data. Your splits should reflect how the model will actually be used in production. If you’ll predict future events, use temporal splits. If you’ll encounter new entities, use group splits. If you’ll serve diverse populations, ensure splits represent that diversity.

As you build machine learning systems, treat data splitting as a critical design decision, not an afterthought. Document your strategy. Validate your splits. Use training data exclusively for learning. Iterate freely on validation data. Touch test data only once. Monitor production performance against test estimates.

Master these practices, and you’ll build models with realistic performance expectations, detect overfitting before deployment, and confidently deploy systems that actually work in the real world. Data splitting might seem simple, but doing it right separates reliable, production-ready machine learning systems from experimental code that only works in notebooks.

The discipline of proper data splitting is fundamental to machine learning success. It’s how we ensure our models don’t just perform well in development, but actually deliver value when deployed to solve real problems with real data.