Introduction to Logistic Regression

Learn Logistic Regression in-depth, from its working principles to advanced applications. Master classification algorithms for machine learning success.

By Techietory on January 11, 2025

Classification algorithms are a cornerstone of machine learning, providing the tools to categorize data into distinct classes. Among the array of classification techniques, Logistic Regression stands out as a simple yet powerful statistical model that effectively solves binary classification problems. Despite its name, Logistic Regression is not a regression algorithm but rather a classification method. It has been widely adopted across industries, from healthcare and finance to marketing and social sciences, due to its interpretability and efficacy. This article delves into the foundational concepts of Logistic Regression, its working mechanism, and why it remains a preferred choice for many data scientists.

Introduction to Classification and Logistic Regression

In machine learning, classification problems involve identifying which category or class a new observation belongs to, based on a set of input features. For example, predicting whether an email is spam or not, determining whether a patient has a disease, or classifying customer reviews as positive or negative are common classification tasks. These tasks require models that can handle categorical outputs effectively.

What Is Logistic Regression?

Logistic Regression is a statistical technique for modeling the relationship between a dependent variable (target) and one or more independent variables (predictors). Unlike Linear Regression, which predicts continuous outcomes, Logistic Regression predicts probabilities that the target belongs to a particular class. The algorithm uses the logistic function, also known as the sigmoid function, to map any real-valued number to a value between 0 and 1, making it ideal for binary classification problems.

The Logistic Function

The logistic function plays a central role in Logistic Regression. It is defined as:

Where:

z = β₀+β₁x₁+β₂x₂+…+β_nx_n (the linear combination of predictors)

e is the base of the natural logarithm.

The output of this function is always a value between 0 and 1, which can be interpreted as the probability of the target belonging to a certain class.

Key Assumptions of Logistic Regression

Before implementing Logistic Regression, it is essential to understand its underlying assumptions:

Binary Outcome: Logistic Regression is best suited for binary classification problems (e.g., yes/no, success/failure).
Linearity of Independent Variables and Log-Odds: The independent variables should have a linear relationship with the log-odds of the dependent variable.
Independence of Observations: The observations in the dataset should be independent of each other.
No Multicollinearity: There should not be a high correlation among the independent variables.

Applications of Logistic Regression

Logistic Regression is widely used in diverse fields due to its simplicity and interpretability:

Healthcare: Predicting the presence or absence of a disease.
Finance: Estimating the probability of loan default or credit card fraud.
Marketing: Classifying customer segments or predicting customer churn.
Social Sciences: Analyzing survey data and categorical outcomes.

These applications highlight the versatility of Logistic Regression in real-world scenarios.

Advantages of Logistic Regression

Simplicity and Interpretability: The coefficients of the model can be easily interpreted as the change in the log-odds of the outcome for a one-unit change in the predictor.
Probabilistic Output: Logistic Regression provides probabilities as outputs, which are valuable for decision-making processes.
Efficient Computation: It is computationally inexpensive and scales well with datasets of varying sizes.
Regularization Options: Extensions like L1 (Lasso) and L2 (Ridge) regularization can handle overfitting and improve generalization.

How Logistic Regression Works

At its core, Logistic Regression estimates the probability of a target variable belonging to a particular class. For binary classification, the target variable y takes values of either 0 or 1. The model predicts the probability P(y = 1 ∣ X), where X represents the input features.

Step 1: The Linear Combination

The model starts by calculating a linear combination of the input features X:

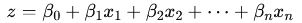
Here:

β₀ is the intercept or bias term.
β₁,β₂,…,β_n are the coefficients corresponding to the input features x₁,x₂,…,x_n.

This linear combination forms the foundation for predicting the outcome.

Step 2: Applying the Sigmoid Function

The logistic function (or sigmoid function) is applied to z to map the result to a probability value between 0 and 1:

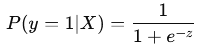
The sigmoid function ensures the output is interpretable as a probability. If P(y = 1 ∣ X) > 0.5, the model predicts the class as 1; otherwise, it predicts 0.

Training a Logistic Regression Model

Training a Logistic Regression model involves finding the optimal values for the coefficients (β₀,β₁,…,β_n) that minimize the difference between the predicted probabilities and the actual target values in the dataset.

1. Cost Function

Instead of using Mean Squared Error (as in Linear Regression), Logistic Regression relies on a cost function tailored for classification tasks:

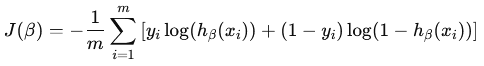
Where:

h_β(x_i) is the predicted probability for the i^th observation.
m is the total number of observations.
y_i is the actual target value for the i^th observation.

This cost function, known as Log Loss or Cross-Entropy Loss, penalizes large deviations between predicted probabilities and actual outcomes.

2. Optimization via Gradient Descent

To minimize the cost function, the algorithm employs Gradient Descent, an iterative optimization technique. The gradient of the cost function with respect to each coefficient is calculated, and the coefficients are updated as follows:

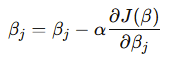
Where:

α is the learning rate, controlling the step size in each iteration.
∂J(β) / ∂β_j is the gradient of the cost function with respect to β_j.

This process continues until the cost function converges to a minimum.

Evaluating Logistic Regression Performance

The effectiveness of a Logistic Regression model is evaluated using metrics tailored to classification problems. Some key metrics include:

1. Accuracy

Accuracy measures the proportion of correctly classified instances out of the total instances:

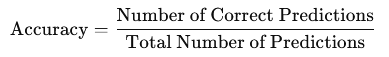
While simple to compute, accuracy may not be the best metric for imbalanced datasets.

2. Precision and Recall

Precision and recall are especially useful for imbalanced datasets:

Precision: The proportion of true positive predictions out of all positive predictions.

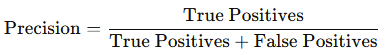
Recall (Sensitivity): The proportion of true positive predictions out of all actual positive instances.

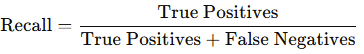
3. F1 Score

The F1 Score is the harmonic mean of precision and recall, providing a single metric that balances the two:

4. ROC-AUC Curve

The Receiver Operating Characteristic (ROC) curve plots the True Positive Rate (TPR) against the False Positive Rate (FPR) at various threshold levels. The Area Under the Curve (AUC) quantifies the model’s ability to distinguish between classes.

Regularization in Logistic Regression

To prevent overfitting, regularization techniques are often applied in Logistic Regression:

L1 Regularization (Lasso): Adds a penalty proportional to the absolute value of the coefficients (|β_j|).
L2 Regularization (Ridge): Adds a penalty proportional to the square of the coefficients (β²_j).

Regularization helps reduce the complexity of the model, ensuring better generalization to unseen data.

Implementation Insights

Logistic Regression can be implemented easily using popular machine learning libraries such as Scikit-learn in Python. Here’s a basic example:

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# Load dataset and split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Initialize and train the model
model = LogisticRegression()
model.fit(X_train, y_train)

# Predict and evaluate
y_pred = model.predict(X_test)
print(f"Accuracy: {accuracy_score(y_test, y_pred)}")

This simplicity, combined with its interpretability and efficiency, makes Logistic Regression a go-to choice for binary classification problems.

Advanced Use Cases of Logistic Regression

While Logistic Regression is often associated with basic binary classification, it is versatile enough to address more complex problems.

1. Multinomial Logistic Regression

Logistic Regression can be extended to solve multiclass classification problems where the target variable has more than two categories. This is achieved using the softmax function instead of the sigmoid function, enabling the model to assign probabilities across multiple classes. Multinomial Logistic Regression is commonly applied in:

Natural Language Processing (NLP): Classifying text into multiple categories (e.g., sentiment analysis with positive, neutral, or negative sentiments).
Image Recognition: Identifying objects in images from a predefined set of classes.

2. Ordinal Logistic Regression

In cases where the target variable has ordered categories (e.g., ratings like poor, average, good), Ordinal Logistic Regression is used. This extension models the cumulative probabilities of the categories while respecting their order.

3. Logistic Regression with Interaction Terms

Adding interaction terms between variables helps capture relationships that are not purely linear. For instance, the combined effect of age and income on loan approval might reveal insights that individual features do not provide.

4. Logistic Regression with Feature Engineering

Feature engineering can significantly enhance the predictive power of Logistic Regression. Techniques include:

Polynomial features to capture non-linear relationships.
Encoding categorical variables using one-hot encoding or label encoding.
Scaling numerical variables to normalize their range.

Limitations of Logistic Regression

Despite its strengths, Logistic Regression has limitations that must be addressed to ensure its effective use:

1. Assumes a Linear Relationship

Logistic Regression assumes a linear relationship between the independent variables and the log-odds of the target variable. For non-linear problems, this assumption limits its applicability.

2. Sensitive to Outliers

Outliers can distort the model’s performance, as they disproportionately influence the coefficients. Addressing this requires outlier detection and removal or using robust scaling techniques.

3. Not Suitable for Complex Relationships

For highly complex datasets with intricate interactions between features, Logistic Regression may underperform compared to more sophisticated algorithms like Random Forests, Gradient Boosting Machines, or Neural Networks.

4. Requires Feature Selection

Logistic Regression does not inherently handle irrelevant or redundant features. Poorly selected features can lead to overfitting or reduced interpretability.

Optimizing Logistic Regression: Practical Tips

To maximize the performance of Logistic Regression, consider the following best practices:

1. Perform Exploratory Data Analysis (EDA)

Visualize the data to identify patterns, trends, and correlations.
Detect and address missing values and outliers.

2. Feature Scaling

Normalize numerical features using standardization (z-score) or Min-Max scaling to improve convergence during training.

3. Use Regularization

Regularization (L1 or L2) is crucial for preventing overfitting, especially when working with high-dimensional datasets.
Use hyperparameter tuning (e.g., grid search or random search) to select the optimal regularization strength (C).

4. Handle Class Imbalance

For imbalanced datasets, where one class significantly outnumbers the other, consider techniques such as:
- Oversampling the minority class (e.g., using SMOTE).
- Undersampling the majority class.
- Using class weights to assign higher importance to the minority class during training.

5. Validate with Cross-Validation

Use techniques like k-fold cross-validation to ensure the model generalizes well to unseen data.

6. Interpret Model Coefficients

Regularly inspect the coefficients to understand the impact of each feature on the target variable.
Use statistical tools like p-values to assess the significance of each predictor.

7. Enhance Non-Linear Relationships

If linearity is a limitation, consider adding polynomial features or switching to algorithms that can model non-linear relationships.

When to Use Logistic Regression

Logistic Regression is ideal when:

Interpretability is crucial: Its coefficients provide clear insights into feature importance.
Data is linearly separable: Logistic Regression performs well when the classes are easily separable.
Efficiency matters: It is computationally efficient, making it suitable for large datasets.

However, for problems requiring high accuracy or involving complex relationships, other machine learning techniques may outperform Logistic Regression.

Conclusion

Logistic Regression is a cornerstone algorithm in the machine learning toolkit, offering simplicity, interpretability, and efficiency for binary classification problems. Its mathematical foundation—the logistic function—provides a probabilistic framework that is both robust and intuitive. From predicting loan defaults in finance to diagnosing diseases in healthcare, Logistic Regression continues to demonstrate its value across industries.

Nevertheless, like any algorithm, it has its limitations. Ensuring the proper application of Logistic Regression involves data preprocessing, regularization, and validation. Furthermore, understanding when to choose Logistic Regression over more complex algorithms is key to leveraging its full potential.

As machine learning evolves, Logistic Regression remains a vital tool for tackling straightforward classification problems. Its role as a baseline model ensures it will continue to be an essential part of any data scientist’s arsenal. Whether you are a beginner or a seasoned professional, mastering Logistic Regression is a step toward building a strong foundation in machine learning.